题目内容
(08年朝阳区综合练习一文)(13分)
设函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,
时,![]() 取得极值,求
取得极值,求![]() 的值;
的值;
(Ⅱ)若![]() 在
在![]() 内为增函数,求
内为增函数,求![]() 的取值范围.
的取值范围.
解析: ![]() ,
,
(Ⅰ)由题意:![]()
解得![]() . …………………3分
. …………………3分
(Ⅱ)方程![]() 的判别式
的判别式![]() ,
,
(1) 当![]() , 即
, 即![]() 时,
时,![]() ,
,
![]() 在
在![]() 内恒成立, 此时
内恒成立, 此时![]() 为增函数;
为增函数;
(2) 当![]() , 即
, 即![]() 或
或![]() 时,
时,
要使![]() 在
在![]() 内为增函数, 只需在
内为增函数, 只需在![]() 内有
内有![]() 即可,
即可,
设![]() ,
,
由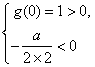 得
得 ![]() , 所以
, 所以![]() .
.
由(1) (2)可知,若![]() 在
在![]() 内为增函数,
内为增函数,![]() 的取值范围是
的取值范围是![]() .………13
.………13

练习册系列答案
相关题目