题目内容
过椭圆 的右焦点F2并垂直于x轴的直线与椭圆的一个交点为B椭圆上不同的两点A(x1,y1)B(x2,y2)满足条件:|F2A||F2B||F2C|成等差数列,则弦AC的中垂线在y轴上的截距的范围是( )
的右焦点F2并垂直于x轴的直线与椭圆的一个交点为B椭圆上不同的两点A(x1,y1)B(x2,y2)满足条件:|F2A||F2B||F2C|成等差数列,则弦AC的中垂线在y轴上的截距的范围是( )A.

B.

C.

D.
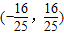
【答案】分析:使用焦半径公式求得x1+x2的值,可以设AC的中垂线方程,代入椭圆方程,使用韦达定理;也可以用“点差法”:记AC中点M(4,y),将A、C两点的坐标代入椭圆方程后作差,求得AC的斜率表达式,表示出AC的中垂线方程,把x=0代入求得AC的中垂线在y轴上的截距,根据M在圆内求得y的范围,进而求得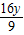 的范围即弦AC的中垂线在y轴上的截距的范围.
的范围即弦AC的中垂线在y轴上的截距的范围.
解答: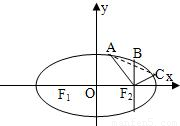 解:对|F2A|+|F2C|=
解:对|F2A|+|F2C|=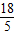
使用焦半径公式得:5- x1+5-
x1+5- x2=
x2=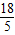 ⇒x1+x2=8.
⇒x1+x2=8.
此后,可以设AC的中垂线方程,代入椭圆方程,使用韦达定理;也可以用“点差”:记AC中点M(4,y),将A、C两点的坐标代入椭圆方程后作差得:
⇒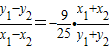 ,
,
∴kAC=-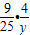 ,
,
于是有:AC的中垂线的方程为:
y-y=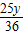 (x-4),
(x-4),
当x=0时:y=-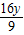 ,此即AC的中垂线在y轴上的截距,
,此即AC的中垂线在y轴上的截距,
∵M(4,y)在椭圆“内”,
∴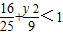 ,
,
得- <y<
<y< ,
,
∴-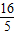 <-
<-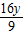 <
<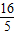 .
.
故选:C.
点评:本题主要考查了椭圆的应用,直线与椭圆的位置关系的综合.当直线与圆锥曲线相交时,涉及弦长问题,常用“韦达定理法”设而不求计算弦长(即应用弦长公式);涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来,相互转化.
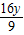 的范围即弦AC的中垂线在y轴上的截距的范围.
的范围即弦AC的中垂线在y轴上的截距的范围.解答:
 解:对|F2A|+|F2C|=
解:对|F2A|+|F2C|=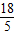
使用焦半径公式得:5-
 x1+5-
x1+5- x2=
x2=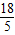 ⇒x1+x2=8.
⇒x1+x2=8.此后,可以设AC的中垂线方程,代入椭圆方程,使用韦达定理;也可以用“点差”:记AC中点M(4,y),将A、C两点的坐标代入椭圆方程后作差得:
⇒
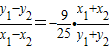 ,
,∴kAC=-
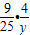 ,
,于是有:AC的中垂线的方程为:
y-y=
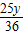 (x-4),
(x-4),当x=0时:y=-
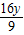 ,此即AC的中垂线在y轴上的截距,
,此即AC的中垂线在y轴上的截距,∵M(4,y)在椭圆“内”,
∴
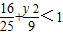 ,
,得-
 <y<
<y< ,
,∴-
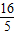 <-
<-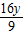 <
<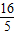 .
.故选:C.
点评:本题主要考查了椭圆的应用,直线与椭圆的位置关系的综合.当直线与圆锥曲线相交时,涉及弦长问题,常用“韦达定理法”设而不求计算弦长(即应用弦长公式);涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来,相互转化.

练习册系列答案
相关题目
以椭圆的右焦点F2为圆心作一个圆,使此圆过椭圆中心O并交椭圆于点M,N,若过椭圆左焦点F1的直线MF1是圆F2的切线,则椭圆的离心率( )
A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
 过椭圆
过椭圆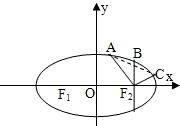 过椭圆
过椭圆 的右焦点F2并垂直于x轴的直线与椭圆的一个交点为B,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列,则弦AC的中垂线在y轴上的截距的范围是 ________.
的右焦点F2并垂直于x轴的直线与椭圆的一个交点为B,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列,则弦AC的中垂线在y轴上的截距的范围是 ________. 的右焦点F2并垂直于x轴的直线与椭圆的一个交点为B,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列,则弦AC的中垂线在y轴上的截距的范围是 .
的右焦点F2并垂直于x轴的直线与椭圆的一个交点为B,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列,则弦AC的中垂线在y轴上的截距的范围是 .