题目内容
已知直线l:x-my+1-m=0(m∈R),圆C:x2+y2+4x-2y-4=0.(Ⅰ)证明:对任意m∈R,直线l与圆C恒有两个公共点.
(Ⅱ)过圆心C作CM⊥l于点M,当m变化时,求点M的轨迹Γ的方程.
(Ⅲ)直线l:x-my+1-m=0与点M的轨迹Γ交于点M,N,与圆C交于点A,B,是否存在m的值,使得
 ?若存在,试求出m的值;若不存在,请说明理由.
?若存在,试求出m的值;若不存在,请说明理由.
【答案】分析:(Ⅰ)方法1:先利用点到直线的距离公式求出圆心C到直线l距离d,然后比较d与圆的半径的大小即可判断
方法2:联立方程组直线与圆的方程,通过判断方程解的个数即可判断直线与圆的位置关系
方法3:将圆x2+y2+4x-2y-4=0化成标准方程,而x-my+1-m=0可得:x+1-m(1+y)=0可求直线恒过定点N(-1,-1).由N在圆C内,可判断直线l与圆的位置关系
(Ⅱ)设CN的中点为D,由题意可知M点的轨迹T为以CN为直径的圆可求轨迹T的方程
(Ⅲ)假设存在满足条件的m,而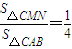 ?
?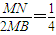 ?
?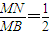 ,利用点到直线的距离公式及直线与圆相交的性质,结合勾股定理即可求解m
,利用点到直线的距离公式及直线与圆相交的性质,结合勾股定理即可求解m
解答:解:(Ⅰ)方法1:圆心C的坐标为(-2,1),半径为3
圆心C到直线l距离d=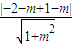 =
=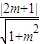
∴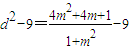
=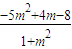 =
=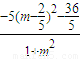 <0
<0
∴d2<9即d<3
∴直线l与圆C恒有两个公共点
方法2:联立方程组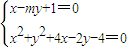
消去x,得(m2+1)y2+(2m2+2m-2)y+(m2+2m-7)=0
△=(2m2+2m-2)2-4(m2+1)(m2+2m-7)=4(5m2+8)>0
∴直线l与圆C恒有两个公共点
方法3:将圆x2+y2+4x-2y-4=0化成标准方程为(x+2)2+(y-1)2=9.
由x-my+1-m=0可得:x+1-m(1+y)=0.
解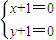 得x=-1,y=-1,所以直线l过定点N(-1,-1).
得x=-1,y=-1,所以直线l过定点N(-1,-1).
因为N在圆C内,所以直线l与圆C恒有两个公共点.
(Ⅱ)设CN的中点为D,由于∠CMN=90°
∴DM= CN
CN
∴M点的轨迹T为以CN为直径的圆.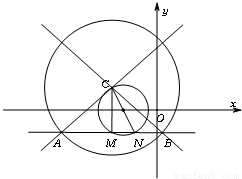
CN中点D的坐标为(-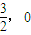 ),
),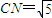 .
.
∴所以轨迹T的方程为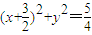
(Ⅲ)假设存在m的值,使得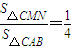 如图所示,有
如图所示,有
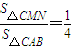 ?
?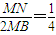 ?
?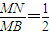 ,
,
又MB2=9-d2,MN2=5-d2,
其中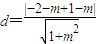 =
=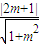 为C到直线L的距离.
为C到直线L的距离.
所以9-d2=4(5-d2),化简得m2+12m-8=0.解得m=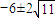 .
.
所以存在m,使得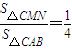 且m=
且m=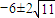 .
.
点评:本题主要考查了直线与圆相交的性质的应用,注意(1)中解题的不同的解法的应用,本题具有一定的综合性
方法2:联立方程组直线与圆的方程,通过判断方程解的个数即可判断直线与圆的位置关系
方法3:将圆x2+y2+4x-2y-4=0化成标准方程,而x-my+1-m=0可得:x+1-m(1+y)=0可求直线恒过定点N(-1,-1).由N在圆C内,可判断直线l与圆的位置关系
(Ⅱ)设CN的中点为D,由题意可知M点的轨迹T为以CN为直径的圆可求轨迹T的方程
(Ⅲ)假设存在满足条件的m,而
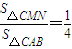 ?
?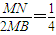 ?
?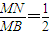 ,利用点到直线的距离公式及直线与圆相交的性质,结合勾股定理即可求解m
,利用点到直线的距离公式及直线与圆相交的性质,结合勾股定理即可求解m解答:解:(Ⅰ)方法1:圆心C的坐标为(-2,1),半径为3
圆心C到直线l距离d=
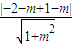 =
=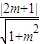
∴
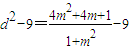
=
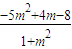 =
=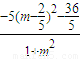 <0
<0∴d2<9即d<3
∴直线l与圆C恒有两个公共点
方法2:联立方程组
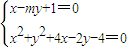
消去x,得(m2+1)y2+(2m2+2m-2)y+(m2+2m-7)=0
△=(2m2+2m-2)2-4(m2+1)(m2+2m-7)=4(5m2+8)>0
∴直线l与圆C恒有两个公共点
方法3:将圆x2+y2+4x-2y-4=0化成标准方程为(x+2)2+(y-1)2=9.
由x-my+1-m=0可得:x+1-m(1+y)=0.
解
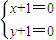 得x=-1,y=-1,所以直线l过定点N(-1,-1).
得x=-1,y=-1,所以直线l过定点N(-1,-1).因为N在圆C内,所以直线l与圆C恒有两个公共点.
(Ⅱ)设CN的中点为D,由于∠CMN=90°
∴DM=
 CN
CN∴M点的轨迹T为以CN为直径的圆.

CN中点D的坐标为(-
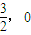 ),
),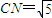 .
.∴所以轨迹T的方程为
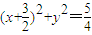
(Ⅲ)假设存在m的值,使得
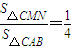 如图所示,有
如图所示,有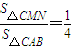 ?
?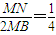 ?
?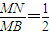 ,
,又MB2=9-d2,MN2=5-d2,
其中
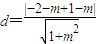 =
=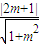 为C到直线L的距离.
为C到直线L的距离.所以9-d2=4(5-d2),化简得m2+12m-8=0.解得m=
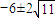 .
.所以存在m,使得
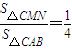 且m=
且m=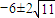 .
.点评:本题主要考查了直线与圆相交的性质的应用,注意(1)中解题的不同的解法的应用,本题具有一定的综合性

练习册系列答案
相关题目
 如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2.
如图,已知直线l:x=my+4(m∈R)与x轴交于点P,交抛物线y2=2ax(a>0)于A,B两点,坐标原点O是PQ的中点,记直线AQ,BQ的斜率分别为k1,k2. (2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0).
(2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0). 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C: