题目内容
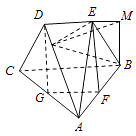
【题目】在多面体ABCDE中,BC=BA,DE∥BC,AE⊥平面BCDE,BC=2DE,F为AB的中点. 
(1)求证:EF∥平面ACD;
(2)若EA=EB=CD,求二面角B﹣AD﹣E的正切值的大小.
【答案】
(1)证明:取AC中点G,连接DG,FG.
因为F是AB的中点,所以FG是△ABC的中位线,
则FG∥BC,FG= ![]() ,
,
所以FG∥DE,FG=DE,
则四边形DEFG是平行四边形,
所以EF∥DG,故EF∥平面ACD.
(2)解:过点B作BM垂直DE的延长线于点M,
因为AE⊥平面BCDE,所以AE⊥BM,则BM⊥平面ADE,
过M作MH⊥AD,垂足为H,连接BH,则AD⊥平面BMH,
所以AD⊥BH,则∠BHM是二面角B﹣AD﹣E的平面角.
设DE=a,则BC=AB=2a,
在△BEM中,EM= ![]() ,BE=
,BE= ![]() ,所以BM=
,所以BM= ![]() .
.
又因为△ADE∽△MDH,
所以HM= ![]() ,则tan∠BHM=
,则tan∠BHM= ![]() .
.
【解析】(1)取AC中点G,连接DG,FG,由已知得四边形DEFG是平行四边形,由此能证明EF∥平面ACD.(2)过点B作BM垂直DE的延长线于点M,过M作MH⊥AD,垂足为H,连接BH,则∠BHM是二面角B﹣AD﹣E的平面角,由此能求出二面角B﹣AD﹣E的正切值的大小.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.

练习册系列答案
相关题目