题目内容
如图,已知一个等腰三角形ABC的顶角B=120°,过AC的一个平面α与顶点B的距离为1,根据已知条件,你能求出AB在平面α上的射影AB1的长吗?如果不能,那么需要增加什么条件,可以使AB1=2?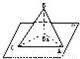
【答案】分析:由于AB不能确定,所以不能求出AB在平面α上的射影AB1的长;需要增加的条件是与三角形ABC有关的长度,夹角等.
解答:解:在条件“等腰△ABC的顶角B=120°”下,
△ABC是不能唯一确定的,这样线段AB1也是不能确定的,
需要增加下列条件之一,可使AB1=2:
①CB1=2;
②CB= 或AB=
或AB=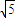 ;
;
③直线AB与平面α所成的角∠BAB1=arcsin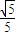 ;
;
④∠ABB1=arctan2;
⑤∠B1AC=arccos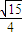 ;
;
⑥∠AB1C=π-arccos ;
;
⑦AC= ;
;
⑧B1到AC的距离为 ;
;
⑨B到AC的距离为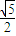 ;
;
⑩二面角B-AC-B1为arctan2等等.
点评:本题考查棱锥的结构特征,是开放题,考查学生逻辑思维能力,是基础题.
解答:解:在条件“等腰△ABC的顶角B=120°”下,
△ABC是不能唯一确定的,这样线段AB1也是不能确定的,
需要增加下列条件之一,可使AB1=2:
①CB1=2;
②CB=
 或AB=
或AB=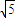 ;
;③直线AB与平面α所成的角∠BAB1=arcsin
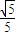 ;
;④∠ABB1=arctan2;
⑤∠B1AC=arccos
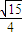 ;
;⑥∠AB1C=π-arccos
 ;
;⑦AC=
 ;
;⑧B1到AC的距离为
 ;
;⑨B到AC的距离为
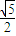 ;
;⑩二面角B-AC-B1为arctan2等等.
点评:本题考查棱锥的结构特征,是开放题,考查学生逻辑思维能力,是基础题.

练习册系列答案
相关题目
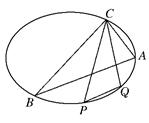
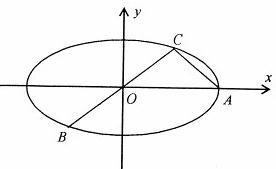 如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且
如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且 如图,已知三棱锥P-ABC的侧面PAC是底角为45°的等腰三角形,PA=PC,且该侧面垂直于底面,∠ACB=90°,AB=10,BC=6,B1C1=3.
如图,已知三棱锥P-ABC的侧面PAC是底角为45°的等腰三角形,PA=PC,且该侧面垂直于底面,∠ACB=90°,AB=10,BC=6,B1C1=3.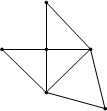

 是长轴为
是长轴为 的椭圆上三点,点
的椭圆上三点,点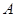 是长轴的一个顶点,
是长轴的一个顶点,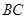 过椭圆中心
过椭圆中心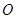 ,且
,且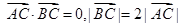 .
.
 使直线
使直线 与
与 轴围成底边在
轴围成底边在 使
使 ?请给出证明.
?请给出证明.