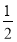题目内容
12.已知函数f(x)=ln(x+1)-$\frac{x}{x+1}$.(1)证明:f(x)≥0;
(2)若当x≥0,f(x)≤ax2恒成立,求实数a的取值范围.
分析 (1)先对原函数求导,从而判断单调性,求其最小值,说明最小值大于或等于零即可;
(2)将问题转化为f(x)-ax2≤0恒成立,然后讨论函数的单调性,求其最值即可使其小于或等于零构造不等式即可.
解答 解:(1)由题意得函数的定义域为(-1,+∞).
f′(x)=$\frac{1}{x+1}-\frac{1}{(x+1)^{2}}=\frac{x}{(x+1)^{2}}$.
当x∈(-1,0)时,f′(x)<0,此时f(x)为减函数;
当x∈(0,+∞)时,f′(x)>0,此时f(x)为增函数.
所以f(x)min=f(0)=0,所以f(x)≥0在定义域内恒成立.
(2)由已知得ln(x+1)-$\frac{x}{x+1}-a{x}^{2}≤0$,当x≥0时恒成立.
令h(x)=ln(x+1)-$\frac{x}{x+1}-a{x}^{2}$,x∈[0,+∞).
则$h′(x)=\frac{1}{x+1}-\frac{1}{(x+1)^{2}}-2ax$=$\frac{x[1-2a(x+1)^{2}]}{(x+1)^{2}}$.
当a≤0时,显然h′(x)≥0恒成立,所以h(x)在定义域内递增,而f(e-1)=lne-$\frac{e-1}{e}-a(e-1)^{2}$=$-a(e-1)^{2}+\frac{1}{e}>0$.故a≤0不符合题意;
当2a≥1即a$≥\frac{1}{2}$时,因为x≥0,故(x+1)2≥1,所以1-2a(x+1)2≤0,故此时h′(x)≤0恒成立,所以h(x)在定义域内递减,所以h(x)max=h(0)=0,
所以此时h(x)≤0在定义域内恒成立,故此时f(x)≤ax2恒成立,所以a$≥\frac{1}{2}$符合题意;
当$0<a<\frac{1}{2}$时,令h′(x)=0得$x=\frac{1}{\sqrt{2a}}-1$>0,
当x$∈(0,\frac{1}{\sqrt{2a}}-1)$时,h′(x)>0,故此时h(x)递增;当x$∈(\frac{1}{\sqrt{2a}},+∞)$时,h′(x)<0,故此时h(x)递减.
而当x→0时,h(x)→ln1=0,结合h(x)此时的单调性,可知函数h(x)不满足在(0,+∞)上恒为负.
综上可知,所求a的范围是[$\frac{1}{2},+∞$).
点评 本题主要考查了利用导数研究函数的单调性,最值的思路;关于不等式恒成立问题,一般转化为函数的最值来解.


| A. | -1006 | B. | 1007 | C. | -1008 | D. | 1009 |
| A. | 50个 | B. | 60个 | C. | 100个 | D. | 120个 |
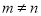 ,两个等差数列
,两个等差数列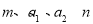 与
与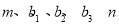 的公差为
的公差为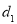 和
和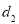 ,则
,则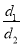 的值为________.
的值为________.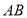 是
是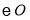 的直径,
的直径,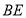 为
为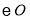 的切线,点
的切线,点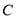 为
为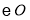 上不同于
上不同于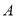 、
、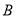 的一点,
的一点,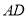 为
为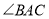 的平分线,且分别与
的平分线,且分别与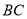 交于
交于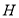 ,与
,与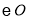 交于
交于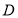 ,与
,与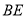 交于
交于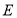 ,连接
,连接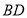 、
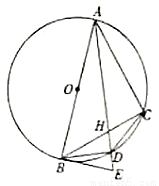
、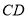 .
.
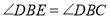 ;
;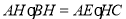 .
.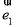 与
与 的夹角为
的夹角为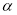 ,且
,且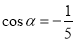 ,若
,若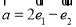 ,
,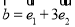 ,则
,则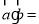 ( )
( )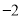 B.
B.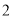
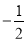 D.
D.