题目内容
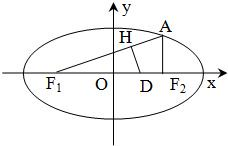如图，椭圆E：| x2 |
| a2 |
| y2 |
| b2 |
| AF2 |
| F1F2 |
| 18 |
| 5 |
（1）求椭圆E的方程；
（2）设点P位椭圆E上的任意一点，求
| PF1 |
| PD |
分析：（1）先根据题意可得c的值和F1、F2的坐标，又因为
•
=0可表示出AF2、AF1，再由sin∠AF1F2=
=
可得到a，b的关系式，最后根据a2=b2+c2可求出a，b的值，确定椭圆方程．
（2）先设点p的坐标，根据其在椭圆上可得到其横纵坐标的关系（用x表示y），然后表示出向量
，
后进行数量积运算得到关于x的二次函数，再由x的取值范围可确定
•
的取值范围．
| AF2 |
| F1F2 |
| DH |
| DF1 |
| AF2 |
| AF1 |
（2）先设点p的坐标，根据其在椭圆上可得到其横纵坐标的关系（用x表示y），然后表示出向量
| PF1 |
| PD |
| PF1 |
| PD |
解答：解：（1）由题意知，c=4，F1（-4，0），F2（4，0），
∵sin∠AF1F2=
=
，DH=
，DF1=6，
又∵
•
=0，
∴AF2=
，AF1=2a-
，
∴
=
，则a2=
b2，
由a2=b2+c2，得b2+16=
b2
∴b2=48，a2=64∴椭圆方程为
+
=1．
（2）设点P（x，y），则
+
=1，即y2=48-
x2
∵
=(-4-X，-Y)，
=(2-x，-y)
∴
•
=x2+y2+2x-8=
x2+2x+40=
(x+4)2+36
∵-8≤x≤8，∴
•
的取值范围是[36，72]．
∵sin∠AF1F2=
| DH |
| DF1 |
| AF2 |
| AF1 |
| 18 |
| 5 |
又∵
| AF2 |
| F1F2 |
∴AF2=
| b2 |
| a |
| b2 |
| a |
∴
| ||
| 6 |
| ||
2a-
|
| 4 |
| 3 |
由a2=b2+c2，得b2+16=
| 4 |
| 3 |
∴b2=48，a2=64∴椭圆方程为
| x2 |
| 64 |
| y2 |
| 48 |
（2）设点P（x，y），则
| x2 |
| 64 |
| y2 |
| 48 |
| 3 |
| 4 |
∵
| PF1 |
| PD |
∴
| PF1 |
| PD |
| 1 |
| 4 |
| 1 |
| 4 |
∵-8≤x≤8，∴
| PF1 |
| PD |
点评：本题主要考查椭圆的基本性质和向量的数量积运算．属基础题．
练习册系列答案
相关题目
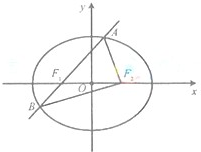（2012•福建）如图，椭圆E：
（2013•深圳二模）如图，椭圆E：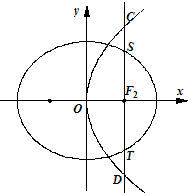
如图，椭圆E：
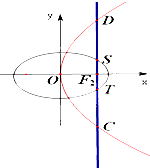（2012•上高县模拟）如图，椭圆