题目内容
已知复数 ,
, (
( ,
, 是虚数单位).
是虚数单位).
(1)若复数 在复平面上对应点落在第一象限,求实数
在复平面上对应点落在第一象限,求实数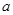 的取值范围;
的取值范围;
(2)若虚数 是实系数一元二次方程
是实系数一元二次方程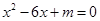 的根,求实数
的根,求实数 值.
值.
(1) ,(2)13.
,(2)13.
解析试题分析:(1)本题解法为按题意列出关于实数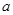 的不等式,解之即可得实数
的不等式,解之即可得实数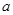 的取值范围. 由条件得,
的取值范围. 由条件得, ,因为
,因为 在复平面上对应点落在第一象限,故有
在复平面上对应点落在第一象限,故有 ∴
∴ 解得
解得 ,(2)因为实系数一元二次方程
,(2)因为实系数一元二次方程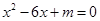 的虚根成对出现,即虚数
的虚根成对出现,即虚数 也是实系数一元二次方程
也是实系数一元二次方程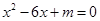 的根,再根据韦达定理列出实数
的根,再根据韦达定理列出实数 的等量关系. 即
的等量关系. 即 ,即
,即 ,把
,把 代入,则
代入,则 ,
, ,所以
,所以 本题也可设
本题也可设 ,代入方程
,代入方程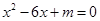 ,利用复数相等列等量关系.
,利用复数相等列等量关系.
(1)由条件得, (2分)
(2分)
因为 在复平面上对应点落在第一象限,故有
在复平面上对应点落在第一象限,故有 (4分)
(4分)
∴ 解得
解得 (6分)
(6分)
(2)因为虚数 是实系数一元二次方程
是实系数一元二次方程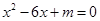 的根
的根
所以 ,即
,即 , (10分)
, (10分)
把 代入,则
代入,则 ,
, , (11分)
, (11分)
所以 (14分)
(14分)
考点:复数方程

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 +(10-a2)i,z2=
+(10-a2)i,z2= +(2a-5)i,若
+(2a-5)i,若 +z2是实数,求实数a的值.
+z2是实数,求实数a的值. 与
与 都是纯虚数,求复数
都是纯虚数,求复数 是方程
是方程 的一个根(
的一个根( 为实数).
为实数). 也是方程的根.
也是方程的根. 是复数,
是复数, 与
与 均为实数,且复数
均为实数,且复数 在复平面上对应的点在第一象限,求实数
在复平面上对应的点在第一象限,求实数 的取值范围.
的取值范围. ,则复数
,则复数
 的值是 .
的值是 .