题目内容
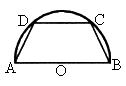
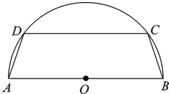 有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
(1)当腰长为1,等腰梯形周长;
(2)设等腰梯形ABCD周长为y,求y的最大值.
解:(1)①代数方法:∵∠ACB=90° CE⊥AB
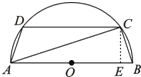
∴BC2=BE•AB
BE=
CD=4-2× =
=
∴周长=4+2+ =
=
②设∠AOD=θ(多种设法)
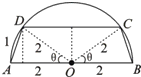
cosθ=
CD2=22+22-2×2×2cos(π-2θ)
=8+8cos2θ=16cos2θ
∴周长=4+2+CD=6+4cosθ=
∴等腰梯形ABCD周长为 (6分)
(6分)
(2)设腰长为x,则BE=
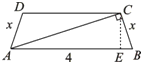
CD=4-2× =4-
=4- y=4+2x+4-
y=4+2x+4-
=- +2x+8(0<x<2
+2x+8(0<x<2 )
)
∴x=2时,ymax=10
∴当等腰梯形的腰长为2时,
周长最大,最大值为10.(12分)
分析:(1)①代数方法:由摄影定理可得BC2=BE•AB结合已知可得BE= ,CD=4-2×
,CD=4-2× =
= ,从而可求
,从而可求
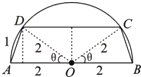
②设∠AOD=θ(多种设法)则cosθ=
利用余弦定理可得CD2=22+22-2×2×2cos(π-2θ)=8+8cos2θ=16cos2θ,从而可得周长=4+2+CD=6+4cosθ=
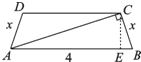
(2)设腰长为x,则BE=
则有CD=4-2× =4-
=4- y=4+2x+4-
y=4+2x+4-
=- +2x+8(0<x<2
+2x+8(0<x<2 ),利用二次函数的知识可求.
),利用二次函数的知识可求.
点评:(1)①摄影定理的应用是解决此题的关键②主要利用的把实际问题转化为利用三角函数的知识解决
(2)二次函数在解决实际问题中求解最值的常用的方法

∴BC2=BE•AB
BE=

CD=4-2×
 =
=
∴周长=4+2+
 =
=
②设∠AOD=θ(多种设法)

cosθ=

CD2=22+22-2×2×2cos(π-2θ)
=8+8cos2θ=16cos2θ
∴周长=4+2+CD=6+4cosθ=

∴等腰梯形ABCD周长为
 (6分)
(6分)(2)设腰长为x,则BE=


CD=4-2×
 =4-
=4- y=4+2x+4-
y=4+2x+4-
=-
 +2x+8(0<x<2
+2x+8(0<x<2 )
)∴x=2时,ymax=10
∴当等腰梯形的腰长为2时,
周长最大,最大值为10.(12分)
分析:(1)①代数方法:由摄影定理可得BC2=BE•AB结合已知可得BE=
 ,CD=4-2×
,CD=4-2× =
= ,从而可求
,从而可求
②设∠AOD=θ(多种设法)则cosθ=

利用余弦定理可得CD2=22+22-2×2×2cos(π-2θ)=8+8cos2θ=16cos2θ,从而可得周长=4+2+CD=6+4cosθ=


(2)设腰长为x,则BE=

则有CD=4-2×
 =4-
=4- y=4+2x+4-
y=4+2x+4-
=-
 +2x+8(0<x<2
+2x+8(0<x<2 ),利用二次函数的知识可求.
),利用二次函数的知识可求.点评:(1)①摄影定理的应用是解决此题的关键②主要利用的把实际问题转化为利用三角函数的知识解决
(2)二次函数在解决实际问题中求解最值的常用的方法

练习册系列答案
相关题目
 如图,半圆形公园上有P和Q两点,线段AB是该半圆的一条直径,C为圆心,半径是2km,现要在公园内建一块顶点都在半圆C上的多边形活动场地为等腰梯形ABPQ.
如图,半圆形公园上有P和Q两点,线段AB是该半圆的一条直径,C为圆心,半径是2km,现要在公园内建一块顶点都在半圆C上的多边形活动场地为等腰梯形ABPQ.