题目内容
设直线 的参数方程为
的参数方程为 (t为参数),若以直角坐标系
(t为参数),若以直角坐标系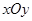 的
的 点为极点,
点为极点, 轴为极轴,选择相同的长度单位建立极坐标系,得曲线
轴为极轴,选择相同的长度单位建立极坐标系,得曲线 的极坐标方程为ρ=
的极坐标方程为ρ=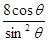 .
.
(1)将曲线 的极坐标方程化为直角坐标方程,并指出曲线是什么曲线;
的极坐标方程化为直角坐标方程,并指出曲线是什么曲线;
(2)若直线 与曲线
与曲线 交于A、B两点,求
交于A、B两点,求 .
.
【答案】
(1) 曲线C表示顶点在原点,焦点在x上的抛物线
(2)10
【解析】
试题分析:解:(1)由ρ=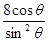 得ρ
得ρ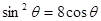
 ∴
∴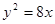
∴ 曲线C表示顶点在原点,焦点在x上的抛物线 (5分)
(2)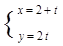 化为
化为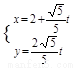 代入
代入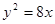 得
得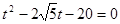
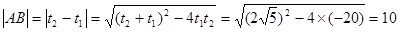 (10分)(或将直线方程化为直角坐标方程用弦长公式求解均可)
(10分)(或将直线方程化为直角坐标方程用弦长公式求解均可)
考点:直线参数方程,极坐标方程
点评:主要是考查了极坐标与直角坐标的互化,以及直线参数方程的运用,属于基础题。

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 (t为参数),点P在直线上,且与点M0(-4,0)的距离为2,如果该直线的参数方程改写成
(t为参数),点P在直线上,且与点M0(-4,0)的距离为2,如果该直线的参数方程改写成 (t为参数),点P在直线上,且与点M0(-4,0)的距离为
(t为参数),点P在直线上,且与点M0(-4,0)的距离为