题目内容
设直线的参数方程为
(t为参数),曲线的极坐标方程为ρ=2
cos(θ+
)
(1)求曲线C的直角坐标方程;
(2)求直线l被曲线C所截得的弦长.
|
| 2 |
| π |
| 4 |
(1)求曲线C的直角坐标方程;
(2)求直线l被曲线C所截得的弦长.
分析:(1)利用极坐标与直角坐标的互化公式
即可得出直角坐标方程;
(2)先把直线的参数方程化为普通方程,观察出直线经过圆心,即可得出弦长为2r.
|
(2)先把直线的参数方程化为普通方程,观察出直线经过圆心,即可得出弦长为2r.
解答:解:(1)∵曲线C的极坐标方程为ρ=2
cos(θ+
),
∴ρ=2cosθ-2sinθ,∴ρ2=2ρcosθ-2ρsinθ,
化为直角坐标方程x2+y2=2x-2y,即为(x-1)2+(y+1)2=2,其圆心C(1,-1),半径r=
.
(2)由直线的参数方程
(t为参数),消去参数t得3x+4y+1=0,
∵圆心C(1,-1)满足直线l的方程3x+4y+1=0,
∴直线l被曲线C所截得的弦长=2r=2
.
| 2 |
| π |
| 4 |
∴ρ=2cosθ-2sinθ,∴ρ2=2ρcosθ-2ρsinθ,
化为直角坐标方程x2+y2=2x-2y,即为(x-1)2+(y+1)2=2,其圆心C(1,-1),半径r=
| 2 |
(2)由直线的参数方程
|
∵圆心C(1,-1)满足直线l的方程3x+4y+1=0,
∴直线l被曲线C所截得的弦长=2r=2
| 2 |
点评:掌握极坐标和直角坐标的互化公式及直线与圆相交的弦长是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (坐标系与参数方程选做题) 设直线
(坐标系与参数方程选做题) 设直线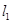 的参数方程为
的参数方程为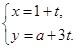 (
(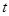 为参数),以坐标原点为极点,x轴为极轴建立极坐标系得另一直线
为参数),以坐标原点为极点,x轴为极轴建立极坐标系得另一直线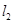 的方程为
的方程为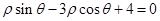 ,
,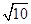 ,则实数
,则实数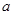 的值为
.
的值为
.