题目内容
若关于x的方程
=kx+2只有一个实数根，则k的取值范围为（ ）
| 4-x2 |
| A、k=0 |
| B、k=0或k＞1 |
| C、k＞1或k＜-1 |
| D、k=0或k＞1或k＜-1 |
分析：观察已知得方程可设方程左边为y1，得出此函数为圆心原点，半径为2的x轴以上半圆，设方程的右边为y2，当k等于0为一个平行于x轴的直线，当k不为0时为一个一次函数，方程只有一个实数根，根据题意画出函数图象，如图所示，即可得到k的取值范围．
解答：
解：根据题意设y1=
，y2=kx+2，
当k=0时，方程只有一个解x=0，满足题意；
当k≠0时，根据题意画出图象，如图所示：
根据图象可知，当k＞1或k＜-1时，直线y=kx+2与y=
只有一个交点，即方程只有一个解，
综上，满足题意k的取值范围为k=0或k＞1或k＜-1．
故选D
解：根据题意设y1=| 4-x2 |
当k=0时，方程只有一个解x=0，满足题意；
当k≠0时，根据题意画出图象，如图所示：
根据图象可知，当k＞1或k＜-1时，直线y=kx+2与y=
| 4-x2 |
综上，满足题意k的取值范围为k=0或k＞1或k＜-1．
故选D
点评：此题考查学生掌握直线与圆的位置关系的判断方法，考查了数形结合的数学思想，是一道中档题．
练习册系列答案
相关题目
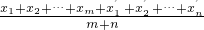的值为
的值为（ ）
的值为（ ）
