题目内容
(1)已知a,b是正数,且a+b=1.求证:(ax+by)(ay+bx)≥xy.(2)若x+3y-1=0,求证:2x+8y≥![]() .
.
证明:(1)左边=(a2+b2)xy+ab(x2+y2)
=[(a+b)2-2ab]xy+ab(x2+y2)
=(1-2ab)xy+ab(x2+y2)
=xy+ab(x-y)2,
∵a>0,b>0,(x-y)2≥0,
∴左边≥xy=右边.
因此不等式成立.
(2)2x+23y≥![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 ”表示一种两个正实数之间的运算,即a
”表示一种两个正实数之间的运算,即a ,a,b是正实
,a,b是正实 =3,则函数
=3,则函数 的值域是
.
的值域是
.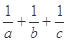 的最小值为( )
的最小值为( )