题目内容
(1)设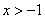 ,试比较
,试比较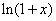 与
与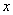 的大小;
的大小;
(2)是否存在常数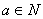 ,使得
,使得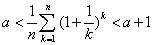 对任意大于
对任意大于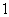 的自然数
的自然数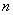 都成立?若存在,试求出
都成立?若存在,试求出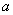 的值并证明你的结论;若不存在,请说明理由。
的值并证明你的结论;若不存在,请说明理由。
【答案】
(Ⅰ)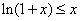 (Ⅱ)
(Ⅱ)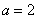 ,利用放缩法证明
,利用放缩法证明
【解析】
试题分析:(Ⅰ)设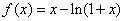 ,则
,则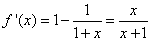 ,
,
当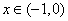 时,
时,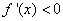 ,
,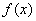 单调递减;
单调递减;
当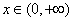 时,
时,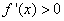 ,
,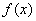 单调递增;
单调递增;
故函数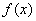 有最小值
有最小值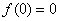 ,则
,则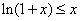 恒成立
4 分
恒成立
4 分
(Ⅱ)取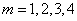 进行验算:
进行验算:
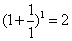
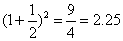
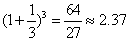
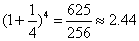
猜测:①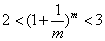 ,
,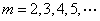
②存在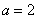 ,使得
,使得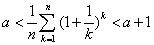 恒成立。
6分
恒成立。
6分
证明一:对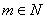 ,且
,且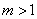 ,
,
有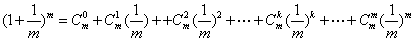
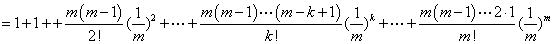
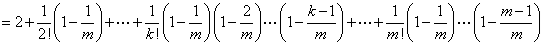
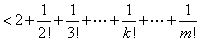
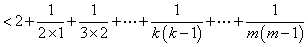
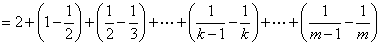
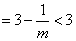
又因 ,
,
故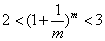 8分
8分
从而有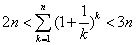 成立,即
成立,即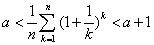
所以存在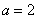 ,使得
,使得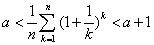 恒成立
10分
恒成立
10分
证明二:
由(1)知:当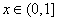 时,
时,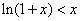 ,
,
设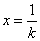 ,
,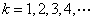 ,
,
则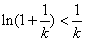 ,所以
,所以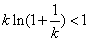 ,
,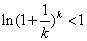 ,
,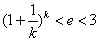 ,
,
当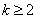 时,再由二项式定理得:
时,再由二项式定理得:
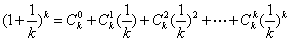
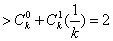
即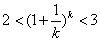 对任意大于
对任意大于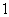 的自然数
的自然数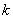 恒成立,
8分
恒成立,
8分
从而有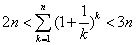 成立,即
成立,即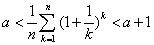
所以存在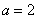 ,使得
,使得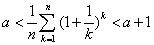 恒成立
10分
恒成立
10分
考点:本题考查了导数的运用及不等式的证明
点评:证明不等式的基本方法有比较法、综合法、分析法。在证明时,关键在于分析待证不等式的结构与特征,选用适当的方法完成不等式的证明

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
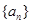 中,公差
中,公差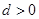 ,其前
,其前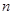 项和为
项和为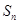 ,且满足
,且满足 ,
,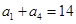 .
.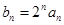 (
( ),求数列
),求数列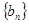 的前
的前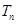 ;
;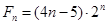 ,试比较
,试比较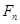 与
与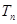 的大小.
的大小.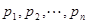 均为正数时,称
均为正数时,称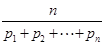 为
为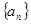 的各项均为正数,且其前
的各项均为正数,且其前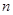 项的“均倒数”为
项的“均倒数”为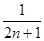 .
.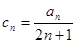
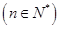 ,试比较
,试比较 与
与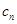 的大小;
的大小;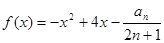 ,是否存在最大的实数
,是否存在最大的实数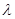 ,使当
,使当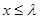 时,对于一切正整数
时,对于一切正整数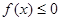 恒成立?
恒成立? 是定义在R上的奇函数,且对任意a、b
是定义在R上的奇函数,且对任意a、b ,当
,当 时,都有
时,都有 .
. ,试比较
,试比较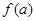 与
与 的大小关系;
的大小关系; 对任意
对任意 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.