题目内容
已知F(-2,0),以F为圆心的圆,半径为r,点A(2,0)是一个定点,P是圆上任意一点,线段AP的垂直平分线l和直线FP相交于点Q.在下列条件下,求点Q的轨迹方程,并说明轨迹是什么曲线.
(1)r=1时,点P在圆上运动;
(2)r=9时,点P在圆上运动.
(1)r=1时,点P在圆上运动;
(2)r=9时,点P在圆上运动.
分析:(1)由题意得QA=QP,则|QA-QF|=|QP-QF|=FP=r=1,即动点Q到两定点F、A的距离差的绝对值为定值,根据双曲线的定义,可得点Q的轨迹是:以F,A为焦点,FA为焦距长的双曲线.
(2)由题意QA=QP,FP=FQ+QP=r=9,所以FQ+QA=9.故曲线是以A、F为焦点,长轴长为9的椭圆,由此能求出曲线的方程.
(2)由题意QA=QP,FP=FQ+QP=r=9,所以FQ+QA=9.故曲线是以A、F为焦点,长轴长为9的椭圆,由此能求出曲线的方程.
解答: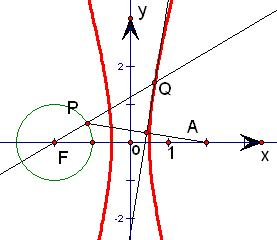 解:(1)当r=1时,
解:(1)当r=1时,
∵A为⊙F外一定点,P为⊙F上一动点
线段AP的垂直平分线交直线FP于点Q,
则QA=QP,则|QA-QF|=|QP-QF|=FP=r=1,
即动点Q到两定点F、A的距离差的绝对值为定值,
根据双曲线的定义,可得点Q的轨迹是:以F,A为焦点,FA为焦距长的双曲线,
故2a=1,2c=4,⇒a=
,c=2,b=
.
故方程为:4x2-
=1(x>0),是双曲线;
 (2)当r=9时,
(2)当r=9时,
由题意:QA=QP,FP=FQ+QP=r=9,
所以FQ+QA=9.
故曲线是以A、F为焦点,长轴长为9的椭圆,
其2a=9,2c=4,⇒a=
,c=2,b=
,
方程为:
+
=1,是椭圆.
 解:(1)当r=1时,
解:(1)当r=1时,∵A为⊙F外一定点,P为⊙F上一动点
线段AP的垂直平分线交直线FP于点Q,
则QA=QP,则|QA-QF|=|QP-QF|=FP=r=1,
即动点Q到两定点F、A的距离差的绝对值为定值,
根据双曲线的定义,可得点Q的轨迹是:以F,A为焦点,FA为焦距长的双曲线,
故2a=1,2c=4,⇒a=
| 1 |
| 2 |
| ||
| 2 |
故方程为:4x2-
| 4y2 |
| 15 |
 (2)当r=9时,
(2)当r=9时,由题意:QA=QP,FP=FQ+QP=r=9,
所以FQ+QA=9.
故曲线是以A、F为焦点,长轴长为9的椭圆,
其2a=9,2c=4,⇒a=
| 9 |
| 2 |
| ||
| 2 |
方程为:
| 4x2 |
| 81 |
| 4y2 |
| 65 |
点评:本小题主要考查椭圆的定义、双曲线的定义、轨迹方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.熟练掌握双曲线、椭圆的定义及圆与直线的性质是解决问题的关键.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
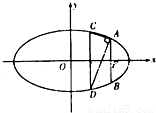
 (2012•潍坊二模)如图,已知F(2,0)为椭圆
(2012•潍坊二模)如图,已知F(2,0)为椭圆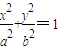 (a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.
(a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.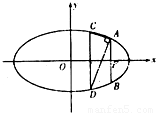
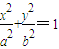 (a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.
(a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.