题目内容
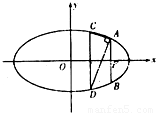
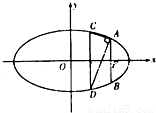
如图,已知F(2,0)为椭圆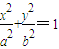 (a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.
(a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.(I)求椭圆的方程;
(II)设过点F斜率为k(k≠0)的直线l与椭圆相交于两点P、Q.若存在一定点E(m,0),使得x轴上的任意一点(异于点E、F)到直线EP、EQ的距离相等,求m的值.
【答案】分析:(Ⅰ)由题意可把A、C、D的坐标用含有a,b的代数式表示,由∠CAD=90°,得到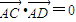 ,代入坐标可得关于a,b的方程,结合a2=b2+4可求解a,b的值,则椭圆方程渴求;
,代入坐标可得关于a,b的方程,结合a2=b2+4可求解a,b的值,则椭圆方程渴求;
(Ⅱ)设出直线l的方程,和椭圆方程联立后化为关于x的一元二次方程,由根与系数关系写出两个交点的横坐标的和与积,由定点E(m,0)使得x轴上的任意一点(异于点E、F)到直线EP、EQ的距离相等得到kEP+kEQ=0,由两点写出斜率代入后再把两根的和与积代入即可求得m的值.
解答:解:(Ⅰ)F(2,0),则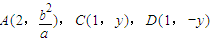 ,其中
,其中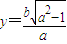 .
.
所以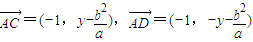 .
.
因为∠CAD=90°,所以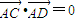 .
.
所以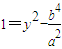 ,即
,即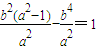 ,
,
联立a2=b2+4解得a2=6,所以b2=2.
可得椭圆方程为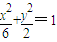 ;
;
(Ⅱ)设P(x1,y1),Q(x2,y2),直线l的方程为y=k(x-2)(k≠0).
由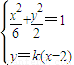 ,得(1+3k2)x2-12k2x+12k2-6=0.
,得(1+3k2)x2-12k2x+12k2-6=0.
所以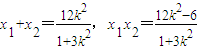 .
.
根据题意,x轴平分∠PEQ,则直线EP,EQ的倾斜角互补,即kEP+kEQ=0.
设E(m,0),则有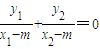 .(当x1=m或x2=m时不合题意)
.(当x1=m或x2=m时不合题意)
将y1=k(x1-2),y2=k(x2-2)代入上式,得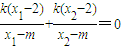 .
.
又k≠0,所以 .
.
即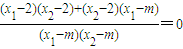 .
.
即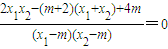 ,
,
∴2x1x2-(m+2)(x1+x2)+4m=0.
将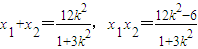 代入,解得m=3.
代入,解得m=3.
点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,考查了数学转化思想方法及学生的运算能力,解答的关键是计算的准确性,是有一定难度题目.
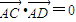 ,代入坐标可得关于a,b的方程,结合a2=b2+4可求解a,b的值,则椭圆方程渴求;
,代入坐标可得关于a,b的方程,结合a2=b2+4可求解a,b的值,则椭圆方程渴求;(Ⅱ)设出直线l的方程,和椭圆方程联立后化为关于x的一元二次方程,由根与系数关系写出两个交点的横坐标的和与积,由定点E(m,0)使得x轴上的任意一点(异于点E、F)到直线EP、EQ的距离相等得到kEP+kEQ=0,由两点写出斜率代入后再把两根的和与积代入即可求得m的值.
解答:解:(Ⅰ)F(2,0),则
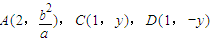 ,其中
,其中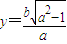 .
.所以
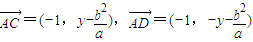 .
.因为∠CAD=90°,所以
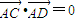 .
.所以
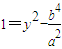 ,即
,即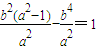 ,
,联立a2=b2+4解得a2=6,所以b2=2.
可得椭圆方程为
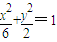 ;
;(Ⅱ)设P(x1,y1),Q(x2,y2),直线l的方程为y=k(x-2)(k≠0).
由
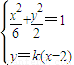 ,得(1+3k2)x2-12k2x+12k2-6=0.
,得(1+3k2)x2-12k2x+12k2-6=0.所以
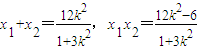 .
.根据题意,x轴平分∠PEQ,则直线EP,EQ的倾斜角互补,即kEP+kEQ=0.
设E(m,0),则有
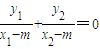 .(当x1=m或x2=m时不合题意)
.(当x1=m或x2=m时不合题意)将y1=k(x1-2),y2=k(x2-2)代入上式,得
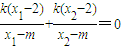 .
.又k≠0,所以
 .
.即
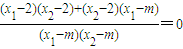 .
.即
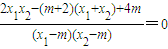 ,
,∴2x1x2-(m+2)(x1+x2)+4m=0.
将
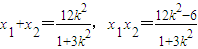 代入,解得m=3.
代入,解得m=3.点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,考查了数学转化思想方法及学生的运算能力,解答的关键是计算的准确性,是有一定难度题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•潍坊二模)如图,已知F(2,0)为椭圆
(2012•潍坊二模)如图,已知F(2,0)为椭圆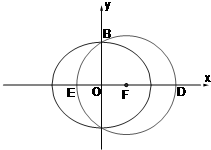 如图,已知F(c,0)是椭圆
如图,已知F(c,0)是椭圆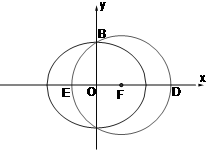 如图,已知F(c,0)是椭圆
如图,已知F(c,0)是椭圆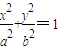 (a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.
(a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.