题目内容
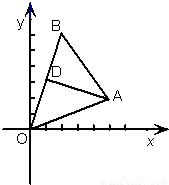
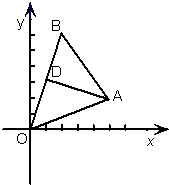 如图在直角坐标系中,点A(5,2),B(2,m)AD⊥OB,垂足为D,
如图在直角坐标系中,点A(5,2),B(2,m)AD⊥OB,垂足为D,(1)若m=6时,求直线AD的方程;
(2)若△AOB的面积为8,求m的值.
分析:(1)由m=6可求B,进而可求KOB,然后由AD⊥OB,结合直线垂直的斜率关系可求AD的斜率,进而可求直线方程
(2)利用两点间的距离公式可求|OB|=
=
,然后求出直线OB的方程,结合点到直线的距离公式可求A到直线OB的距离,代入三角形的面积公式可求
(2)利用两点间的距离公式可求|OB|=
| (x2-x1)2+(y2-y1)2 |
| 4+m2 |
解答:解:(1)当m=6时,B(2,6)-------(1分)
∴kOB=
=
=3-------(3分)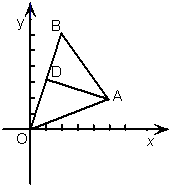
∵AD⊥OB
∴kOB×kAD=-1-------(4分)
∴kAD=-
--------(5分)
根据点斜式可得:y-2=-
(x-5)
即直线AD的方程为:x+3y-11=0-----(6分)
(2)∵|OB|=
=
---(7分)
而直线OB的方程为:y=
x----(8分)
故A到直线OB的距离h=
----(9分)
∴S△AOB=
×h×|OB|=
×|5m-4|=8-----(10分)
解得:m=4或m=-
-----(12分)
∴kOB=
| y2-y1 |
| x2-x1 |
| 6-0 |
| 2-0 |

∵AD⊥OB
∴kOB×kAD=-1-------(4分)
∴kAD=-
| 1 |
| 3 |
根据点斜式可得:y-2=-
| 1 |
| 3 |
即直线AD的方程为:x+3y-11=0-----(6分)
(2)∵|OB|=
| (x2-x1)2+(y2-y1)2 |
| 4+m2 |
而直线OB的方程为:y=
| m |
| 2 |
故A到直线OB的距离h=
| |5m-4| | ||
|
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
解得:m=4或m=-
| 12 |
| 5 |
点评:本题主要考查了直线垂直的斜率关系的应用,直线的点斜式方程的应用及点到直线的距离公式的简单应用.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:
某小学五年级一次考试中,五名同学的语文、英语成绩如表所示: (2013•深圳一模)一次考试中,五名同学的数学、物理成绩如下表所示:
(2013•深圳一模)一次考试中,五名同学的数学、物理成绩如下表所示: