题目内容
在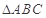 中,已知角
中,已知角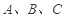 的对边分别为
的对边分别为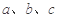 .向量
.向量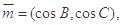
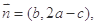 且向量
且向量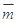 与
与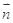 共线.
共线.
(Ⅰ)求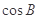 的值;
的值;
(Ⅱ)若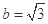 ,求
,求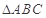 的面积的最大值.
的面积的最大值.
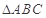 中,已知角
中,已知角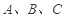 的对边分别为
的对边分别为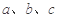 .向量
.向量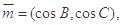
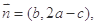 且向量
且向量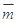 与
与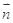 共线.
共线.(Ⅰ)求
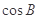 的值;
的值;(Ⅱ)若
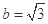 ,求
,求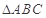 的面积的最大值.
的面积的最大值. (Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
 ;(Ⅱ)
;(Ⅱ) .
.试题分析:(Ⅰ)由向量
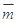 与
与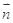 共线得,
共线得, ,这个等式中既有边又有角,这种等式一般有两种考虑:要么只留边,要么只留角.在本题中这两种方法都行.
,这个等式中既有边又有角,这种等式一般有两种考虑:要么只留边,要么只留角.在本题中这两种方法都行.思路一、由正弦定理得:
 ,然后用三角函数公式可求出
,然后用三角函数公式可求出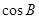 .
.思路二、由余弦定理得:
 ,化简得
,化简得 .再由余弦定理可得
.再由余弦定理可得 .
.(II)由
 可求出
可求出 .这样三角形ABC的面积可表示为
.这样三角形ABC的面积可表示为 .
.要求它的最大值,可考虑求出
 的最大值.因为已知
的最大值.因为已知 和
和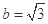 ,所以应该用余弦定理,这样可得:
,所以应该用余弦定理,这样可得: ,即
,即 .从而问题得以解决.
.从而问题得以解决.试题解析:(Ⅰ)法一、由
 得,
得, ,
,所以
 .
.由正弦定理得:
 ,
,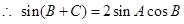 ,
,又
 ,
, .
.又
 .
.法二、由向量
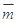 与
与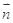 共线得,
共线得, .
.由余弦定理得:
 ,化简得:
,化简得: ,
,即


 .
.所以
 . 6分
. 6分(II)因为
 ,
, .
.由余弦定理得:
 ,即
,即 .
. . 12分
. 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
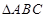 中,角
中,角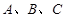 的对边分别为
的对边分别为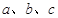 ,且满足
,且满足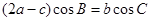 .
.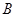 的大小;
的大小;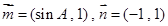 ,求
,求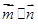 的最小值.
的最小值.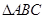 中,角
中,角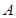 、
、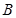 、
、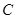 的对边分别为
的对边分别为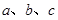 ,且
,且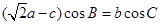 .
. ,且
,且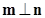 ,求
,求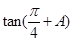 的值.
的值.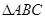 的外接圆半径
的外接圆半径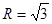 ,角
,角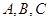 的对边分别是
的对边分别是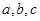 ,且
,且
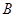 和边长
和边长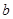 ;
;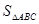 的最大值及取得最大值时的
的最大值及取得最大值时的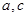 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状.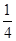 B.
B.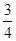 C.
C.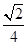 D.
D.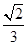
 ,A、B、C成等差数列,则角C=( )
,A、B、C成等差数列,则角C=( ) B.
B. C.
C.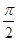 D.
D. 中,角A,B,C所对的边分别是
中,角A,B,C所对的边分别是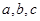 ,且
,且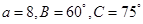 ,
,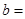 .
. 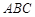 中,角
中,角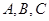 的对边分别为
的对边分别为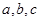 ,若
,若 ,则
,则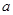 等于
等于 .
.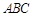 中,
中,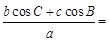 .
.