题目内容
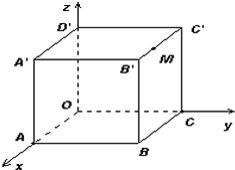 如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 ________.
如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 ________.
(2a,3a,3a)
分析:由图形可知,M点在正方体的上底面上,M点的纵标同D′的纵标相同,M在面BCC′B′上,得到点的竖标为3a,根据M点在这条棱上的位置,写出M点的横标.
解答:由图形可知,M点在正方体的上底面上,
∴M点的纵标同D′的纵标相同,
M在面BCC′B′上,得到点的竖标为3a,
∵C′M=2MB′,
∴M点的横标是2a,
∴M点的坐标是(2a,3a,3a)
故答案为:(2a,3a,3a)
点评:本题考查空间中点的坐标,是一个基础题,解题时借助于点在正方体的一条棱上,写出横标,纵标和竖标,注意各个坐标的符号.
分析:由图形可知,M点在正方体的上底面上,M点的纵标同D′的纵标相同,M在面BCC′B′上,得到点的竖标为3a,根据M点在这条棱上的位置,写出M点的横标.
解答:由图形可知,M点在正方体的上底面上,
∴M点的纵标同D′的纵标相同,
M在面BCC′B′上,得到点的竖标为3a,
∵C′M=2MB′,
∴M点的横标是2a,
∴M点的坐标是(2a,3a,3a)
故答案为:(2a,3a,3a)
点评:本题考查空间中点的坐标,是一个基础题,解题时借助于点在正方体的一条棱上,写出横标,纵标和竖标,注意各个坐标的符号.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目