题目内容
已知集合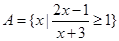 ,
,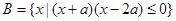 ,其中a>0.
,其中a>0.
(1)求集合A;(2)若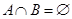 ,求实数a的取值范围
,求实数a的取值范围
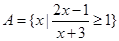 ,
,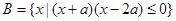 ,其中a>0.
,其中a>0.(1)求集合A;(2)若
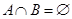 ,求实数a的取值范围
,求实数a的取值范围(1) (2)
(2)
 (2)
(2)
分析:
(1)集合A即{x|(x-4)/(x+3)≥0},解此分式不等式求得集合A。
(2)由 a>0,求得 B={x|-a≤x≤2a},若A∩B=?,则有 -a≥-3且2a<4,
解答:
(1)集合A={x|(x-4)/(x+3)≥0},则x+3≠0且(x-4)(x+3)
因此:{x|x≥4,或 x<-3}。
(2)∵a>0,B={x|(x+a)(x-2a)≤0}={x|-a≤x≤2a},若A∩B=?,则有 -a≥-3且2a<4,解得 a<2,又a>0,
故实数a的取值范围为(0,2)。
点评:本题主要考查集合关系中参数的取值范围问题,分式不等式的解法,两个集合的交集的定义和求法,体现了等价转化的数学思想,属于基础题。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 ,x∈R},则A∩B等于 ( )
,x∈R},则A∩B等于 ( )
 ,
, ,则
,则 ( )
( )



 ,B={x|x2-2x-m<0},
,B={x|x2-2x-m<0}, ,
, ,则
,则 为
为 )
)
 ( )
( )
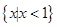
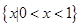
 ,
, ,则
,则 ( )
( )

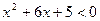 },B={x|?1≤x<1},
},B={x|?1≤x<1},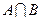 ; (2)若全集U=
; (2)若全集U=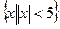 ,求CU(A∪B);
,求CU(A∪B);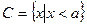 ,且
,且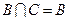 ,求
,求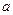 的取值范围.
的取值范围. ,函数
,函数 的定义域为集合
的定义域为集合
 求集合
求集合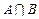 ;
; 且
且 是
是 的必要条件,求实数
的必要条件,求实数 的取值范围.
的取值范围.