题目内容
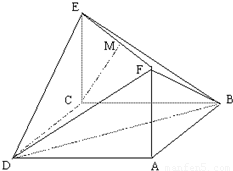
(理)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,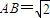 ,
,AF=1,M是线段EF的中点.
(1)求证:CM∥平面BDF;
(2)求二面角A-DB-F的大小.
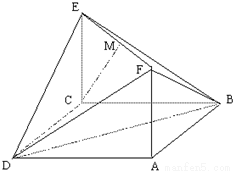
【答案】分析:(1)建立空间直角坐标系,用坐标表示点与向量,证明CM与平面BDF的法向量垂直,即可证得结论;
(2)由(1)知平面BDF的一个法向量为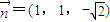 ,平面ABD的一个法向量为
,平面ABD的一个法向量为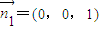 ,从而可求向量
,从而可求向量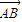 与向量
与向量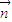 的夹角,即可求得所求二面角A-DB-F的大小.
的夹角,即可求得所求二面角A-DB-F的大小.
解答:(1)证明:建立如图所示的空间直角坐标系,则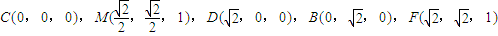 …(2分)
…(2分)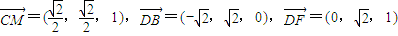
设平面DBF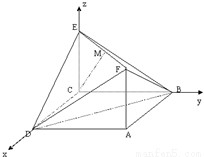 的一个法向量为
的一个法向量为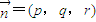 ,则
,则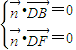 ,
,
∴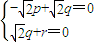
取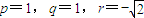 ,
,
得平面DBF的一个法向量为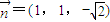 ,…(6分)
,…(6分)
因为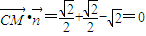 ,
,
所以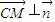 ,
,
又因为直线CM?平面DBF内,所以CM∥平面BDF.…(6分)
(2)解:由(1)知平面BDF的一个法向量为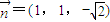 ,
,
而平面ABD的一个法向量为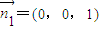 ,
,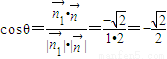 ,…(11分)
,…(11分)
所以向量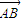 与向量
与向量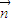 的夹角
的夹角 ,
,
从图中可以看出二面角A-DB-F为锐二面角,所以所求二面角A-DB-F的大小是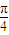 . …(12分)
. …(12分)
点评:本题考查线面平行,考查面面角,解题的关键是建立空间直角坐标系,用坐标表示点与向量,利用向量的数量积求解.
(2)由(1)知平面BDF的一个法向量为
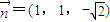 ,平面ABD的一个法向量为
,平面ABD的一个法向量为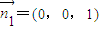 ,从而可求向量
,从而可求向量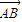 与向量
与向量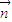 的夹角,即可求得所求二面角A-DB-F的大小.
的夹角,即可求得所求二面角A-DB-F的大小.解答:(1)证明:建立如图所示的空间直角坐标系,则
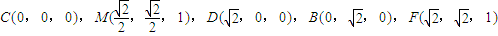 …(2分)
…(2分)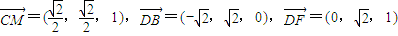
设平面DBF
 的一个法向量为
的一个法向量为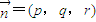 ,则
,则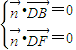 ,
,∴
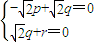
取
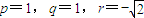 ,
,得平面DBF的一个法向量为
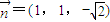 ,…(6分)
,…(6分)因为
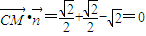 ,
,所以
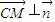 ,
,又因为直线CM?平面DBF内,所以CM∥平面BDF.…(6分)
(2)解:由(1)知平面BDF的一个法向量为
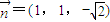 ,
,而平面ABD的一个法向量为
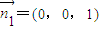 ,
,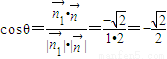 ,…(11分)
,…(11分)所以向量
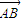 与向量
与向量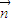 的夹角
的夹角 ,
,从图中可以看出二面角A-DB-F为锐二面角,所以所求二面角A-DB-F的大小是
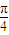 . …(12分)
. …(12分)点评:本题考查线面平行,考查面面角,解题的关键是建立空间直角坐标系,用坐标表示点与向量,利用向量的数量积求解.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
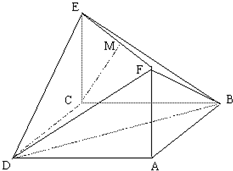 (理)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,
(理)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,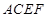 的边
的边 与正方形
与正方形 所在平面垂直,
所在平面垂直, ,
, ,
,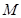 是线段
是线段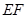 的中点。
的中点。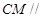 平面
平面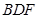
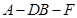 的大小。
的大小。
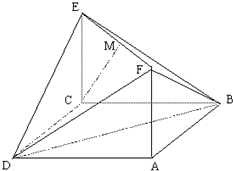 (理)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,
(理)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,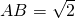 ,
,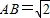 ,
,