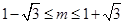题目内容
已知函数f(x)= , 对任意m∈[-3,3],不等式f(mx-1)+f(2x)<0恒成立,则实数x的取值范围为( )
, 对任意m∈[-3,3],不等式f(mx-1)+f(2x)<0恒成立,则实数x的取值范围为( )
A.(-1, ) ) | B.(-2, ) ) | C.(-2, ) ) | D.(-2, ) ) |
A
解析试题分析:因为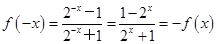 ,故
,故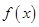 为奇函数,又
为奇函数,又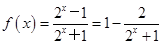 ,而
,而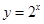 为增函数,故
为增函数,故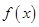 也为增函数,故对任意m∈[-3,3],不等式f(mx-1)+f(2x)<0恒成立,可化为,对任意m∈[-3,3],不等式
也为增函数,故对任意m∈[-3,3],不等式f(mx-1)+f(2x)<0恒成立,可化为,对任意m∈[-3,3],不等式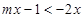 恒成立,即
恒成立,即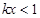 恒成立,其中
恒成立,其中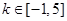 ,令
,令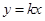 ,画出如下图形,只要
,画出如下图形,只要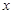 的取值在
的取值在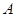 点横坐标和
点横坐标和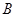 点横坐标之间则题意成立,而
点横坐标之间则题意成立,而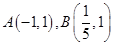 ,故
,故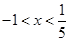 ,选A.
,选A.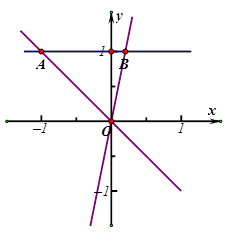
考点:函数奇偶性增减性、函数构造、数形结合.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
对于函数 与
与 和区间D,如果存在
和区间D,如果存在 ,使
,使 ,则称
,则称 是函数
是函数 与
与 在区间D上的“友好点”.现给出两个函数:
在区间D上的“友好点”.现给出两个函数:
① ,
, ;②
;② ,
, ;③
;③ ,
, ;④
;④
 ,
, ,则在区间
,则在区间 上的存在唯一“友好点”的是( )
上的存在唯一“友好点”的是( )
| A.①② | B.③④ | C.②③ | D.①④ |
已知函数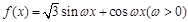 ,
,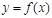 的图像与直线
的图像与直线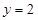 的两个相邻交点的距离等于
的两个相邻交点的距离等于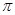 ,则
,则 的单调递增区间是( )
的单调递增区间是( )
A. |
B. |
C.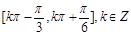 |
D.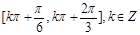 |
设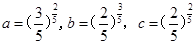 ,则
,则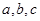 的大小关系是 ( )
的大小关系是 ( )
A.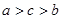 | B.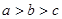 | C.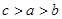 | D.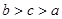 |
若函数 为偶函数,则
为偶函数,则 ( )
( )
A. | B. | C. | D. |
给定映射 ,在映射
,在映射 下
下 中与
中与 中元素
中元素 的对应元素为( )
的对应元素为( )
A. | B. | C. | D. |
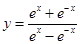 的图像大致为( )
的图像大致为( )
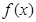 的定义域为
的定义域为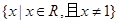 , 且
, 且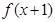 奇函数.当
奇函数.当 时,
时,  -
-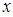 -1,那么函数
-1,那么函数 时,
时, 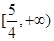
 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足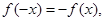 称
称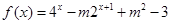 为定义域
为定义域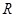 上的“局部奇函数”,则实数的取值范围是( )
上的“局部奇函数”,则实数的取值范围是( )