题目内容
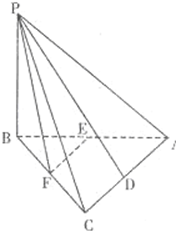 (2012•广安二模)如图,在三棱锥P-ABC中,PB⊥面ABC,∠ABC=90°,AB=BC=2,∠PAB=45°,点D,E,F分别是AC,AB,BC的中点.
(2012•广安二模)如图,在三棱锥P-ABC中,PB⊥面ABC,∠ABC=90°,AB=BC=2,∠PAB=45°,点D,E,F分别是AC,AB,BC的中点.(1)求证:EF⊥PD;
(2)求直线PF与平面PBD所成的角的大小;
(3)求二面角E-PF-B的大小.
分析:(1)连接BD,证明PB⊥平面ABC,从而PD⊥AC,根据E、F分别为AB、BC的中点,可得EF∥AC,从而可得EF⊥PD;
(2)因为面PBD⊥面ABC,故只需过F作BD的垂线,因为EF⊥BD,交点为O,则∠FPO为直线PF与平面PBD所成的角,求解即可;
(3)过B作BM⊥PF于点M,连接EM,证明∠EMB为二面角E-PF-B的平面角,再在直角△PBF中,可求二面角E-PF-B的正切值,从而可得结论.
(2)因为面PBD⊥面ABC,故只需过F作BD的垂线,因为EF⊥BD,交点为O,则∠FPO为直线PF与平面PBD所成的角,求解即可;
(3)过B作BM⊥PF于点M,连接EM,证明∠EMB为二面角E-PF-B的平面角,再在直角△PBF中,可求二面角E-PF-B的正切值,从而可得结论.
解答:(1)证明:连接BD
在△ABC中,∠ABC=90°
∵AB=BC,点D为AC的中点,∴BD⊥AC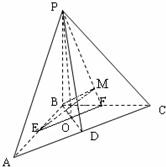
∵PB⊥平面ABC,∴BD为PD在平面ABC内的射影
∴PD⊥AC
∵E、F分别为AB、BC的中点,∴EF∥AC
∴EF⊥PD;
(2)∵PB⊥平面ABC,∴PB⊥EF.
连接BD交EF于点O,∵EF⊥PB,EF⊥PD,∴EF⊥平面PBD,
∴∠FPO为直线PF与平面PBD所成的角,EF⊥PO.
∵PB⊥面ABC,∴PB⊥AB,PB⊥BC,又∵∠PAB=45°,
∴PB=AB=2.
在Rt△FPO中,OF=
AC=
,PF=
=
∴sin∠FPO=
=
∴直线PF与平面PBD所成的角为arcsin
;
(3)过点B作BM⊥PF于点F,连接EM,
∵AB⊥PB,AB⊥BC,
∴AB⊥平面PBC,即BM为EM在平面PBC内的射影,
∴EM⊥PF,
∴∠EMB为二面角E-PF-B的平面角.
∵Rt△PBF中,BM=
=
∴tan∠EMB=
=
∴二面角E-PF-B的大小为arctan
.
在△ABC中,∠ABC=90°
∵AB=BC,点D为AC的中点,∴BD⊥AC

∵PB⊥平面ABC,∴BD为PD在平面ABC内的射影
∴PD⊥AC
∵E、F分别为AB、BC的中点,∴EF∥AC
∴EF⊥PD;
(2)∵PB⊥平面ABC,∴PB⊥EF.
连接BD交EF于点O,∵EF⊥PB,EF⊥PD,∴EF⊥平面PBD,
∴∠FPO为直线PF与平面PBD所成的角,EF⊥PO.
∵PB⊥面ABC,∴PB⊥AB,PB⊥BC,又∵∠PAB=45°,
∴PB=AB=2.
在Rt△FPO中,OF=
| 1 |
| 4 |
| ||
| 2 |
| PB2+BF2 |
| 5 |
∴sin∠FPO=
| OF |
| PF |
| ||
| 10 |
∴直线PF与平面PBD所成的角为arcsin
| ||
| 10 |
(3)过点B作BM⊥PF于点F,连接EM,
∵AB⊥PB,AB⊥BC,
∴AB⊥平面PBC,即BM为EM在平面PBC内的射影,
∴EM⊥PF,
∴∠EMB为二面角E-PF-B的平面角.
∵Rt△PBF中,BM=
| PB•BF |
| PF |
| 2 | ||
|
∴tan∠EMB=
| EB |
| BM |
| ||
| 2 |
∴二面角E-PF-B的大小为arctan
| ||
| 2 |
点评:本题考查线面垂直、线线垂直,考查线面角,面面角,解题的关键是正确运用线面垂直的判断,正确作出线面角,面面角.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目