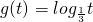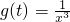题目内容
对函数f（x）=x3+ax2+bx+c作代换x=g（t），则总不会改变函数f（x）的值域的代换是（ ）
A．g(t)=log
| B．g（t）=2t | C．g（t）=sint | D．g(t)=
|
根据题意：函数f（x）的定义域是R，
要求总不改变f（x）值域，则变换后的函数g（t）的值域为R
A、由对数函数的性质知g（t）的值域为R
B、由指数函数的性质知g（t）的值域为（0，+∞）
C，由正弦函数的性质知g（t）的值域为[-1，1]
D、由幂函数的性质知g（t）的值域为（-∞，0）∪（0，+∞）
故选A．
要求总不改变f（x）值域，则变换后的函数g（t）的值域为R
A、由对数函数的性质知g（t）的值域为R
B、由指数函数的性质知g（t）的值域为（0，+∞）
C，由正弦函数的性质知g（t）的值域为[-1，1]
D、由幂函数的性质知g（t）的值域为（-∞，0）∪（0，+∞）
故选A．
练习册系列答案
相关题目
