题目内容
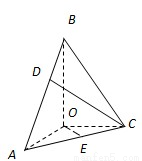
如图,在三棱锥B-ACO中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥B-ACO的体积为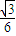 .
.(1)求三棱锥B-ACO的高;
(2)在线段AB上取一点D,当D在什么位置时,
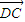 和
和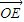 的夹角大小为arccos
的夹角大小为arccos .
.
【答案】分析:(1)由题意的BO⊥平面ACO,即BO就是三棱锥B-ACO的高,然后根据体积建立等式关系,解之即可求出所求;
(2)以O为原点,OA为x轴,OC为y轴,OB为z轴,建立空间直角坐标系,设D(x,0, (1-x)),设
(1-x)),设 和
和 的夹角为θ,则coaθ=
的夹角为θ,则coaθ=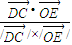 =
= 建立等式关系,解之即可求出x的值,从而可判定点D的位置.
建立等式关系,解之即可求出x的值,从而可判定点D的位置.
解答: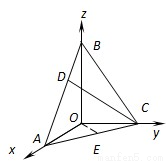 解:(1)由题意的BO⊥平面ACO,即BO就是三棱锥B-ACO的高,…(2分)
解:(1)由题意的BO⊥平面ACO,即BO就是三棱锥B-ACO的高,…(2分)
在Rt△ABO中,设AO=a,∠BAO=60°,所以BO= a,
a,
CO=a,所以VB-ACO= ×
× ×AO×BO×CO=
×AO×BO×CO= a3=
a3= .
.
所以a=1,所以三棱锥的高BO为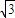 .…(4分)
.…(4分)
(2)以O为原点,如图建立空间直角坐标系…(5分)
设D(x,0,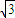 (1-x)),则C(0,1,0),E(
(1-x)),则C(0,1,0),E( ,
, ,0 )
,0 )
 =(-x,1,
=(-x,1, ( x-1)),
( x-1)),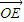 =(
=( ,
, ,0)…(10分)
,0)…(10分)
设 和
和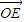 的夹角为θ
的夹角为θ
则coaθ=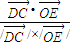
= =
= …(12分)
…(12分)
解之得,x=2(舍去)或x= ,
,
所以当D在AB的中点时,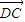 和
和 的夹角大小为arccos
的夹角大小为arccos .…(14分)
.…(14分)
点评:本题主要考查了锥体的体积,以及利用空间向量解决空间两异面直线所成角,同时考查了空间想象能力,推理论证的能力,属于中档题.
(2)以O为原点,OA为x轴,OC为y轴,OB为z轴,建立空间直角坐标系,设D(x,0,
 (1-x)),设
(1-x)),设 和
和 的夹角为θ,则coaθ=
的夹角为θ,则coaθ=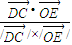 =
= 建立等式关系,解之即可求出x的值,从而可判定点D的位置.
建立等式关系,解之即可求出x的值,从而可判定点D的位置.解答:
 解:(1)由题意的BO⊥平面ACO,即BO就是三棱锥B-ACO的高,…(2分)
解:(1)由题意的BO⊥平面ACO,即BO就是三棱锥B-ACO的高,…(2分)在Rt△ABO中,设AO=a,∠BAO=60°,所以BO=
 a,
a,CO=a,所以VB-ACO=
 ×
× ×AO×BO×CO=
×AO×BO×CO= a3=
a3= .
.所以a=1,所以三棱锥的高BO为
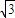 .…(4分)
.…(4分)(2)以O为原点,如图建立空间直角坐标系…(5分)
设D(x,0,
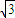 (1-x)),则C(0,1,0),E(
(1-x)),则C(0,1,0),E( ,
, ,0 )
,0 ) =(-x,1,
=(-x,1, ( x-1)),
( x-1)),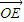 =(
=( ,
, ,0)…(10分)
,0)…(10分)设
 和
和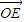 的夹角为θ
的夹角为θ则coaθ=
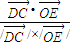
=
 =
= …(12分)
…(12分)解之得,x=2(舍去)或x=
 ,
,所以当D在AB的中点时,
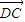 和
和 的夹角大小为arccos
的夹角大小为arccos .…(14分)
.…(14分)点评:本题主要考查了锥体的体积,以及利用空间向量解决空间两异面直线所成角,同时考查了空间想象能力,推理论证的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
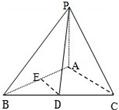 如图,在三棱锥P-ABC中,D、E分别是BC、AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是( )
如图,在三棱锥P-ABC中,D、E分别是BC、AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是( )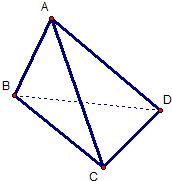 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD= 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4. 如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.
如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC. 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,