题目内容
设 是定义在
是定义在 上的函数,且对任意
上的函数,且对任意 ,当
,当 时,都有
时,都有 ;
;
(1)当 时,比较
时,比较 的大小;
的大小;
(2)解不等式 ;
;
(3)设 且
且 ,求
,求 的取值范围。
的取值范围。
【答案】
(1) ;(2)
;(2)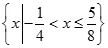 ;(3)
;(3)
【解析】
试题分析:
解:(1)由 对任意
对任意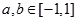 ,当
,当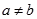 时,都有
时,都有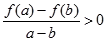 可得:
可得:  在
在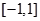 上为单调增函数,因为
上为单调增函数,因为 ,所以,
,所以, ……………………3分
……………………3分
(2)由题意及(1)得: 解得
解得 ,所以不等式
,所以不等式
的解集为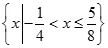 …………………………………………………………9分
…………………………………………………………9分
(3)由题意得: 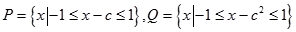 即:
即:
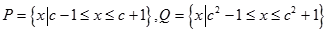
又因为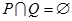 ,所以,
,所以,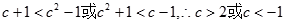
所以, 的取值范围是
的取值范围是 ……………………………………………………12分
……………………………………………………12分
考点:利用定义判定抽象函数单调性,利用单调性解不等式,集合的关系
点评:利用单调性解不等式的时候注意考虑定义域。

练习册系列答案
相关题目
 是定义在
是定义在 上的函数,且
上的函数,且 ,当
,当 时,
时, ,那么当
,那么当 时,
时, 在给定区间M上存在正数t,使得对于任意
在给定区间M上存在正数t,使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的3级类增函数
上的3级类增函数 上的1级类增函数
上的1级类增函数 上的
上的 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2 是定义
是定义 在上的函数,且满足:1.对任意
在上的函数,且满足:1.对任意 ,恒有
,恒有 ;2.对任意
;2.对任意 ,恒有
,恒有 ;3. 对任意
;3. 对任意 ,
, ,若函数
,若函数 上的t级类增函数,则实数t的取值范围为
上的t级类增函数,则实数t的取值范围为 。
。