题目内容
若函数 在给定区间M上存在正数t,使得对于任意
在给定区间M上存在正数t,使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 为M上的t级类增函数。给出4个命题
为M上的t级类增函数。给出4个命题
①函数 上的3级类增函数
上的3级类增函数
②函数 上的1级类增函数
上的1级类增函数
③若函数 上的
上的 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2
④设 是定义
是定义 在上的函数,且满足:1.对任意
在上的函数,且满足:1.对任意 ,恒有
,恒有 ;2.对任意
;2.对任意 ,恒有
,恒有 ;3. 对任意
;3. 对任意 ,
, ,若函数
,若函数 是
是 上的t级类增函数,则实数t的取值范围为
上的t级类增函数,则实数t的取值范围为 。
。
以上命题中为真命题的是
【答案】
①④
【解析】
试题分析:因为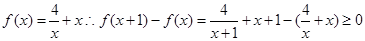 在
在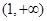 不成立,故A不正确;,∵f(x)=|log2(x-1)|,,∴f(x+1)-f(x)=|log2x|-|log2(x-1)|
不成立,故A不正确;,∵f(x)=|log2(x-1)|,,∴f(x+1)-f(x)=|log2x|-|log2(x-1)|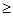 0在(1,+∞)上不成立,故B不正确;∵函数f(x)=sinx+ax为[
0在(1,+∞)上不成立,故B不正确;∵函数f(x)=sinx+ax为[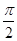 ,+∞)上的
,+∞)上的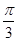 级类增函数,
级类增函数,
∴sin(x+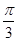 )+a(x+
)+a(x+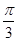 )≥sinx+ax,∴sinxcos
)≥sinx+ax,∴sinxcos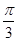 +cosxsin
+cosxsin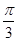 +ax+
+ax+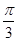 a≥sinx+ax,∴
a≥sinx+ax,∴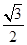 cosx+
cosx+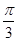 a≥
a≥
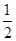 sinx,当x=
sinx,当x=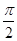 时,
时,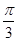 a≥
a≥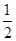 ,a≥
,a≥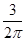 ,∴实数a的最小值不为2,故C不正确;∵f(x)=x2-3x为[1,+∞)上的t级类增函数,∴(x+t)2-3(x+t)≥x2-3x,∴2tx+t2-3t≥0, t≥3-2x∈[1,+∞),故D成立.故答案①④
,∴实数a的最小值不为2,故C不正确;∵f(x)=x2-3x为[1,+∞)上的t级类增函数,∴(x+t)2-3(x+t)≥x2-3x,∴2tx+t2-3t≥0, t≥3-2x∈[1,+∞),故D成立.故答案①④
考点:命题的真假
点评:本题考查命题的真假判断,是中档题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 在给定区间M上存在正数t,使得对于任意
在给定区间M上存在正数t,使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的3级类增函数
上的3级类增函数 上的1级类增函数
上的1级类增函数 上的
上的 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2 是定义
是定义 在上的函数,且满足:1.对任意
在上的函数,且满足:1.对任意 ,恒有
,恒有 ;2.对任意
;2.对任意 ,恒有
,恒有 ;3. 对任意
;3. 对任意 ,
, ,若函数
,若函数 上的t级类增函数,则实数t的取值范围为
上的t级类增函数,则实数t的取值范围为 。
。 上的1级类增函数
上的1级类增函数 上的
上的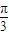 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2