题目内容
8、已知m，n，l是直线，α、β是平面，下列命题中，正确的命题是
①若l垂直于α内两条直线，则l⊥α；
②若l平行于α，则α内可有无数条直线与l平行；
③若m⊥n，n⊥l则m∥l； ④若m?α，l?β，且α∥β，则m∥l．
②
．（填序号）①若l垂直于α内两条直线，则l⊥α；
②若l平行于α，则α内可有无数条直线与l平行；
③若m⊥n，n⊥l则m∥l； ④若m?α，l?β，且α∥β，则m∥l．
分析：若l垂直于α内两条平行直线，则l不垂直于α．故①不成立；若l平行于α，则l平行于α内所有直线，故②成立；若m⊥n，n⊥l，则m与l平行、相交或异面，故③不成立；若m?α，l?β，且α∥β，则m与l平行、相交或异面，故④不成立．
解答：解：①：若l垂直于α内两条相交直线，则l⊥α；若l垂直于α内两条平行直线，则l不垂直于α．故①不成立．
②若l平行于α，则l平行于α内所有直线，故②成立；
③若m⊥n，n⊥l，则m与l平行、相交或异面，故③不成立；
④若m?α，l?β，且α∥β，则m与l平行、相交或异面，故④不成立．
故答案为：②．
②若l平行于α，则l平行于α内所有直线，故②成立；
③若m⊥n，n⊥l，则m与l平行、相交或异面，故③不成立；
④若m?α，l?β，且α∥β，则m与l平行、相交或异面，故④不成立．
故答案为：②．
点评：本题考查命题的真假判断与应用，解题时要注意立体几何性质的合理应用和真假命题的正确判断．
练习册系列答案
相关题目
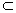α，则l∥α；
β，则m⊥l；