题目内容
已知函数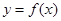 是R上的偶函数,对于任意
是R上的偶函数,对于任意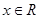 都有
都有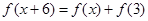 成立,当
成立,当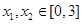 ,且
,且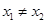 时,都有
时,都有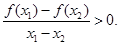 给出下列命题:
给出下列命题:
①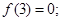 ②直线
②直线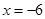 是函数
是函数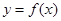 的图像的一条对称轴;
的图像的一条对称轴;
③函数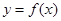 在[-9,-6]上为增函数; ④函数
在[-9,-6]上为增函数; ④函数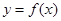 在[-9,9]上有4个零点。
在[-9,9]上有4个零点。
其中正确的命题为. (将所有正确命题的编号都填上)
【答案】
①②④
【解析】
试题分析:取 ,得
,得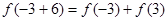 ,而
,而 ,
,
所以 ,命题①正确;从而已知条件可化为
,命题①正确;从而已知条件可化为 ,
,
于是

 ,所以
,所以 是其一条对称轴,命题②正确;因为当
是其一条对称轴,命题②正确;因为当 ,且
,且 时,都有
时,都有 ,所以此时单调递增,从而
,所以此时单调递增,从而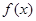 在
在 上单调递减,又从上述过程可知原函数的周期为6,从而当
上单调递减,又从上述过程可知原函数的周期为6,从而当 时,
时,
 ,
, ,此时为减函数,所以命题③错误;同理,
,此时为减函数,所以命题③错误;同理,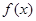 在[3,6]上单调递减,所以只有
在[3,6]上单调递减,所以只有
 ,得命题④正确.综上所述,正确命题的序号为①②④.
,得命题④正确.综上所述,正确命题的序号为①②④.
考点:函数的奇偶性单调性周期性等性质的考查
点评:函数的性质的考查一直以来都是热点,尤其以奇偶性单调性周期性最为常见,求解本题的入手点在于通过 中x的恰当的赋值得到周期性及图像过的特殊点
中x的恰当的赋值得到周期性及图像过的特殊点

练习册系列答案
相关题目