题目内容
设集合S中的元素为实数，且满足条件：①S内不含
1；②若
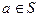，则必有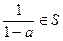
。
（I）证明：若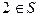
，则S中必存在另外两个元素，并求出这两个元素。
（II）集合S中的元素能否有且只有一个？为什么
？
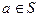1；②若，则必有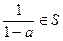。（I）证明：若
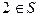，则S中必存在另外两个元素，并求出这两个元素。（II）集合S中的元素能否有且只有一个？为什么
？见解析
（I）证明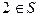：∵，且由条件②知：
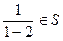，则
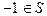
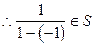，即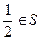
∴S中必存在另外两个元素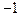
和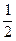
（II）解：若S中只有一个元素a，则由条件②得：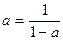
，且
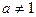
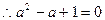，又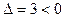
， ∴此方程无实数解
∴集合S不可能是单元素集合
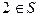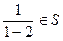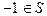
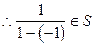，且由条件②知：，则，即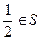 ∴S中必存在另外两个元素
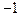和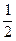（II）解：若S中只有一个元素a，则由条件②得：
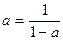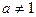
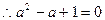，且，又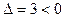， ∴此方程无实数解∴集合S不可能是单元素集合
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
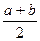，给出下列四个算式：
曲线F(x,y)+λG(x,y)=0(λ为常数)过点P(x0,y0),则A是B的__________条件.
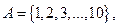求集合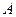
的所有非空子集元素和的和。
，
，
，求集合
．
﹑
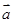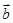均为非零向量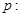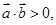，条件
条件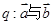
的夹角为锐角，则
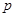是
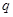成立的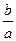
,1}，也可表示为{a
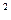,a+b ,0}，则a
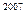+b