题目内容
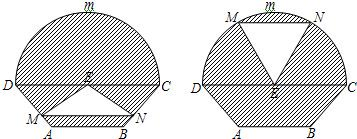 如图所示的自动通风设施.该设施的下部ABCD是等腰梯形,其中AB=1米,高0.5米,CD=2a(a>
如图所示的自动通风设施.该设施的下部ABCD是等腰梯形,其中AB=1米,高0.5米,CD=2a(a>| 1 | 2 |
(1)设MN与AB之间的距离为x米,试将三角通风窗EMN的通风面积S(平方米)表示成关于x的函数S=f(x);
(2)当MN与AB之间的距离为多少米时,三角通风窗EMN的通风面积最大?并求出这个最大面积.
分析:(1)如图当通风窗在CD下方时,即0≤x<
时,由平面几何知识,得
=
,可得MN=2(2a-1)x+1,再由三角形面积公式建立面积模型.当通风窗在CD的上方时,即
<x<a+
时,则MN=2
,再由三角形面积公式建立面积模型.,
(2)根据分段函数,分别求得每段上的最大值,最后取它们当中最大的,即为原函数的最大值,并明确取值的状态,从而得到实际问题的建设方案.
| 1 |
| 2 |
| MN-1 |
| 2a-1 |
| x | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
a2-(x-
|
(2)根据分段函数,分别求得每段上的最大值,最后取它们当中最大的,即为原函数的最大值,并明确取值的状态,从而得到实际问题的建设方案.
解答:解:(1)当0≤x<
时,由平面几何知识,得
=
.
∴MN=2(2a-1)x+1,
∴S=f(x)=-(2a-1)x2+(a-1)x+
.(3分)
当
<x<a+
时,S=f(x)=
•2
•(x-
)
=
•(x-
),
∴S=f(x)=
(5分)
(2)当0≤x<
时,S=f(x)=-(2a-1)x2+(a-1)x+
.
∵a>
,
∴
-
=
<0,
∴
<
.
①
<a≤1,当x=0时,[f(x)]max=f(0)=
.
②a>1,当x=
时,[f(x)]max=f[
]=
.(7分)
当
<x<a+
时,S=f(x)=
•2
•(x-
)
=
•(x-
)=
≤
=
a2,
等号成立?(x-
)2=a2-(x-
)2?x=
(
a+1)∈(
,a+
).
∴当x=
(
a+1)时,[f(x)]max=
.(10分)
当
<a≤1时,∵
-
=
(a+
)(a-
),
∴
<a≤
时.当x=0,[f(x)]max=f(0)=
,
<a≤1时,
当x=
(
a+1),[f(x)]max=
.(12分)
a>1时,
a2-
=
a2>0.
当x=
(
a+1)时,[f(x)]max=
.
综上,
<a≤
时,当x=0时,[f(x)]max=f(0)=
,
即MN与AB之间的距离为0米时,三角通风窗EMN的通风面积最大,最大面积为
平方米.a>
时,
当x=
(
a+1)时,[f(x)]max=
,即MN与AB之间的距离为x=
(
a+1)米时,
三角通风窗EMN的通风面积最大,最大面积为
a2平方米.(16分)
| 1 |
| 2 |
| MN-1 |
| 2a-1 |
| x | ||
|
∴MN=2(2a-1)x+1,
∴S=f(x)=-(2a-1)x2+(a-1)x+
| 1 |
| 4 |
当
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
a2-(x-
|
| 1 |
| 2 |
=
a2-(x-
|
| 1 |
| 2 |
∴S=f(x)=
|
(2)当0≤x<
| 1 |
| 2 |
| 1 |
| 4 |
∵a>
| 1 |
| 2 |
∴
| a-1 |
| 2(2a-1) |
| 1 |
| 2 |
| -a |
| 2(2a-1) |
∴
| a-1 |
| 2(2a-1) |
| 1 |
| 2 |
①
| 1 |
| 2 |
| 1 |
| 4 |
②a>1,当x=
| a-1 |
| 2(2a-1) |
| a-1 |
| 2(2a-1) |
| a2 |
| 4(2a-1) |
当
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
a2-(x-
|
| 1 |
| 2 |
=
a2-(x-
|
| 1 |
| 2 |
(x-
|
(x-
| ||||
| 2 |
| 1 |
| 2 |
等号成立?(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
| 2 |
| a2 |
| 2 |
当
| 1 |
| 2 |
| a2 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| ||
| 2 |
当x=
| 1 |
| 2 |
| 2 |
| a2 |
| 2 |
a>1时,
| 1 |
| 2 |
| a2 |
| 4(2a-1) |
| 4a-3 |
| 4(2a-1) |
当x=
| 1 |
| 2 |
| 2 |
| a2 |
| 2 |
综上,
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
即MN与AB之间的距离为0米时,三角通风窗EMN的通风面积最大,最大面积为
| 1 |
| 4 |
| ||
| 2 |
当x=
| 1 |
| 2 |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
| 2 |
三角通风窗EMN的通风面积最大,最大面积为
| 1 |
| 2 |
点评:本题主要考查函数模型的建立与应用,主要涉及了平面图形中的相似比,三角形面积公式,分段函数求最值以及二次函数法,基本不等式法,作差法等解题方法.

练习册系列答案
相关题目
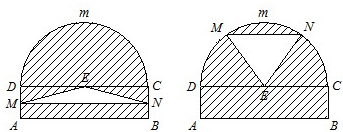 (2009•普陀区二模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合).
(2009•普陀区二模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆(MN和AB、DC不重合).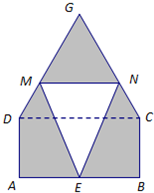 (2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.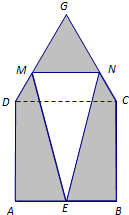 (2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是正方形,其中AB=2米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是正方形,其中AB=2米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆. 是等腰梯形,其中
是等腰梯形,其中 米,梯形的高为
米,梯形的高为 米,
米, 米,上部
米,上部 是个半圆,固定点
是个半圆,固定点 为
为 的中点.△
的中点.△ 是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),
是由电脑控制其形状变化的三角通风窗(阴影部分均不通风), 是可以沿设施边框上下滑动且始终保持和
是可以沿设施边框上下滑动且始终保持和 之间的距离为
之间的距离为 米,试将三角通风窗
米,试将三角通风窗 (平方米)表示成关于
(平方米)表示成关于 ;
;