��Ŀ����
 ��2009•��������ģ��ij�ֿ�Ϊ�˱��ֿ��ڵ�ʪ�Ⱥ��¶ȣ�����ǽ�Ͼ�װ����ͼ��ʾ���Զ�ͨ����ʩ������ʩ���²�ABCD�Ǿ��Σ�����AB=2�ף�BC=0.5�ף��ϲ�CmD�Ǹ���Բ���̶���EΪCD���е㣮��EMN���ɵ��Կ�������״�仯������ͨ�細����Ӱ���־���ͨ�磩��MN�ǿ�������ʩ�߿����»�����ʼ�ձ��ֺ�ABƽ�е�������ˣ�MN��AB��DC���غϣ���
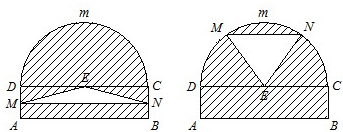
��2009•��������ģ��ij�ֿ�Ϊ�˱��ֿ��ڵ�ʪ�Ⱥ��¶ȣ�����ǽ�Ͼ�װ����ͼ��ʾ���Զ�ͨ����ʩ������ʩ���²�ABCD�Ǿ��Σ�����AB=2�ף�BC=0.5�ף��ϲ�CmD�Ǹ���Բ���̶���EΪCD���е㣮��EMN���ɵ��Կ�������״�仯������ͨ�細����Ӱ���־���ͨ�磩��MN�ǿ�������ʩ�߿����»�����ʼ�ձ��ֺ�ABƽ�е�������ˣ�MN��AB��DC���غϣ�����1����MN��AB֮��ľ���Ϊ1��ʱ�����ʱ����ͨ�細EMN��ͨ�������
��2����MN��AB֮��ľ���Ϊx�ף��Խ�����ͨ�細EMN��ͨ�����S��ƽ���ף���ʾ�ɹ���x�ĺ���S=f��x����
��3����MN��AB֮��ľ���Ϊ������ʱ������ͨ�細EMN��ͨ����������������������
��������1����MN��AB֮��ľ���Ϊ1��ʱ��MNӦλ��DC�Ϸ����Ҵ�ʱ��EMN��MN���ϵĸ�Ϊ0.5�ף��Ӷ�����MN�ij����������������ʽ�����
��2����MN�ھ��������ڻ�������x��(0��
)ʱ���������������ʽ�������ģ�ͣ���MN�ڰ�Բ�������ڻ�������x��(
��
)ʱ���������������ʽ�������ģ�ͣ�
��3�����ݷֶκ������ֱ����ÿ���ϵ����ֵ�����ȡ���ǵ������ģ���Ϊԭ���������ֵ������ȷȡֵ��״̬���Ӷ��õ�ʵ������Ľ��跽����
��2����MN�ھ��������ڻ�������x��(0��
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
��3�����ݷֶκ������ֱ����ÿ���ϵ����ֵ�����ȡ���ǵ������ģ���Ϊԭ���������ֵ������ȷȡֵ��״̬���Ӷ��õ�ʵ������Ľ��跽����
����⣺��1�������⣬��MN��AB֮��ľ���Ϊ1��ʱ��MNӦλ��DC�Ϸ����Ҵ�ʱ��EMN��MN���ϵĸ�Ϊ0.5�ף�����ΪEM=EN=1�ף�����MN=
�ף�����S��EMN=
ƽ������������ͨ�細EMN��ͨ�����Ϊ
ƽ����
��2����MN�ھ��������ڻ�������x��(0��
)ʱ����EMN�����S=
��MN��(
-x)=
-x��
��MN�ڰ�Բ�������ڻ�������x��(
��
)ʱ����EMN�����S=(x-
)•
���Ͽɵ�S=f(x)=
��
��3����MN�ھ��������ڻ���ʱ��f��x��������(0��
)�ϵ����ݼ�����f��x����f��0��=
��
��MN�ڰ�Բ�������ڻ�����f(x)=(x-
)•
��
=
�Ⱥų���ʱ��x=
(
+1)
��˵�x=
(
+1)���ף�ʱ��ÿ�������εõ����ͨ�����Ϊ
ƽ���ף�
| 3 |
| ||
| 4 |
| ||
| 4 |
��2����MN�ھ��������ڻ�������x��(0��
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��MN�ڰ�Բ�������ڻ�������x��(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
1-(x-
|
���Ͽɵ�S=f(x)=
|
��3����MN�ھ��������ڻ���ʱ��f��x��������(0��
| 1 |
| 2 |
| 1 |
| 2 |
��MN�ڰ�Բ�������ڻ�����f(x)=(x-
| 1 |
| 2 |
1-(x-
|
(x-
| ||||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
��˵�x=
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
������������Ҫ���麯��ģ�͵Ľ�����Ӧ�ã���Ҫ�漰�������������ʽ���ֶκ�������ֵ�Լ���������ʽ���Ƚ��ⷽ����

��ϰ��ϵ�д�
 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�
�����Ŀ