题目内容
数列{an}满足:an=3an-1+3n-1(n∈N,n≥2),其中a4=365,
(1)求a1,a2,a3; (2)若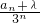 为等差数列,求常数λ的值;(3)求{an}的前n项和Sn.
为等差数列,求常数λ的值;(3)求{an}的前n项和Sn.
解:(1)a1=5,a2=23,a3=95
(2)由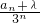 为等差数列可得:
为等差数列可得:
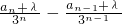 为常数,
为常数,
即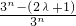 为常数,
为常数,
所以2λ+1=0,
故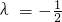
(3)由2)可得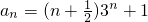
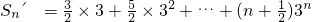
3Sn′= ×3n+1
×3n+1
∴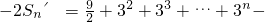
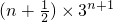
所以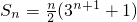
分析:(1)令数列的递推关系中的n依次取4,3,2,通过解方程求出a1,a2,a3;
(2)求出数列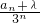 的第n项减去第n-1项求出差,由于差为常数,令2λ+1=0,求出常数λ的值.
的第n项减去第n-1项求出差,由于差为常数,令2λ+1=0,求出常数λ的值.
(3)利用等差数列的通项公式先求出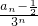 的通项,通过解方程求出an,利用错位相减法求出前n项和.
的通项,通过解方程求出an,利用错位相减法求出前n项和.
点评:求数列的前n项和时,应该先求出通项,判断出通项的特点,再选择合适的求和方法.
(2)由
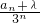 为等差数列可得:
为等差数列可得: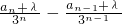 为常数,
为常数,即
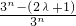 为常数,
为常数,所以2λ+1=0,
故
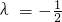
(3)由2)可得
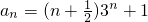
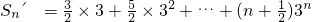
3Sn′=
 ×3n+1
×3n+1∴
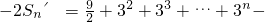
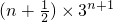
所以
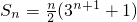
分析:(1)令数列的递推关系中的n依次取4,3,2,通过解方程求出a1,a2,a3;
(2)求出数列
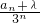 的第n项减去第n-1项求出差,由于差为常数,令2λ+1=0,求出常数λ的值.
的第n项减去第n-1项求出差,由于差为常数,令2λ+1=0,求出常数λ的值.(3)利用等差数列的通项公式先求出
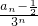 的通项,通过解方程求出an,利用错位相减法求出前n项和.
的通项,通过解方程求出an,利用错位相减法求出前n项和.点评:求数列的前n项和时,应该先求出通项,判断出通项的特点,再选择合适的求和方法.

练习册系列答案
相关题目