题目内容
已知数列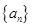 满足:
满足: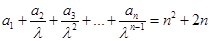 (其中常数
(其中常数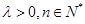 ).
).
(1)求数列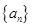 的通项公式;
的通项公式;
(2)当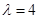 时,数列
时,数列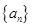 中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。
中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。
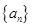 满足:
满足: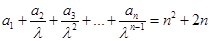 (其中常数
(其中常数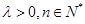 ).
).(1)求数列
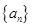 的通项公式;
的通项公式;(2)当
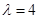 时,数列
时,数列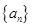 中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。
中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。(1)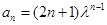 (2)不存在这样的三项使其组成等比数列
(2)不存在这样的三项使其组成等比数列
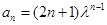 (2)不存在这样的三项使其组成等比数列
(2)不存在这样的三项使其组成等比数列试题分析:(1)当
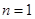 时,
时,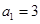 ,
,当
 时,因为
时,因为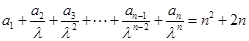
所以:

两式相减得到:
 ,即
,即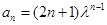 ,又
,又 ,
,所以数列
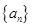 的通项公式是
的通项公式是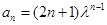 ;
;(2)当
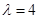 时,
时, ,假设存在
,假设存在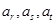 成等比数列,
成等比数列,则
 .
.整理得
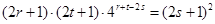 .
.由奇偶性知
 r+t-2s=0.
r+t-2s=0.所以
 ,即
,即 ,这与
,这与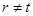 矛盾,
矛盾,故不存在这样的正整数
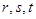 ,使得
,使得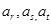 成等比数列.
成等比数列. 点评:第一小题是由数列的前n项和求通项,需注意分
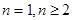 两种情况讨论,第二小题探索性题目,先假设满足题意要求的项存在,看是否能推得矛盾,若无矛盾则假设成立,反之假设不成立
两种情况讨论,第二小题探索性题目,先假设满足题意要求的项存在,看是否能推得矛盾,若无矛盾则假设成立,反之假设不成立
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 满足:
满足: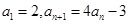 ,则
,则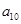 等于 ( )
等于 ( )



 中,
中, ,前三项和
,前三项和 ,则公比
,则公比 的值为
的值为 或
或
 或
或
 ,则
,则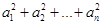 等于( )
等于( )
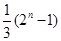
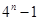
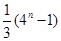
 是等比数列
是等比数列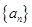 的前n项和,
的前n项和,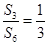 ,则
,则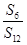 等于( )
等于( )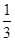
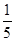

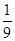
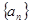 中,已知
中,已知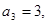
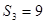 ,则
,则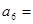 ( )
( )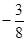
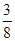
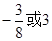
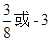
 ABC中,
ABC中, 为
为 的对边,且
的对边,且 ,则( )
,则( )  成等差数列
成等差数列 ,周三、周四两天,每天上涨
,周三、周四两天,每天上涨
 中, 若
中, 若 是方程
是方程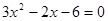 的两根,则
的两根,则 =___________.
=___________.