题目内容
下列函数中,既是奇函数,又是增函数是
- A.f(x)=x|x|
- B.f(x)=-x3
- C.f(x)=
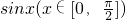
- D.f(x)=

A
分析:四个选项中都给出了具体的函数解析式,其中选项A是分段函数,可由f(-x)=-x|-x|=-x|x|=-f(x)知函数为奇函数,在分析x>0时函数的增减性,根据奇函数的对称性进一步得到函数在整个定义域内的增减性;
选项B举一反例即可;
C、D中的两个函数,定义域均不关于原点对称,都不是奇函数.
解答:由f(-x)=-x|-x|=-x|x|=-f(x),知函数f(x)=x|x|为奇函数,又f(x)=x|x|=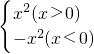 当x>0时,f(x)=x2在(0,∞)上为增函数,根据奇函数图象关于原点中心对称,
当x>0时,f(x)=x2在(0,∞)上为增函数,根据奇函数图象关于原点中心对称,
所以当x<0时,f(x)=-x2在(-∞,0)上也为增函数,所以函数f(x)=x|x|在定义域内既是奇函数,又是增函数,故A正确.
∵2>1,而-23<-13,所以函数f(x)=x3在定义域内不是增函数,故B不正确.
∵ 不关于原点对称,∴f(x)=sinx
不关于原点对称,∴f(x)=sinx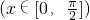 在给定的定义域内不是奇函数,故C不正确.
在给定的定义域内不是奇函数,故C不正确.
∵f(x)= 的定义域为{x|x>0},不关于原点对称,所以函数f(x)=
的定义域为{x|x>0},不关于原点对称,所以函数f(x)= 在定义域内不是奇函数,故D不正确.
在定义域内不是奇函数,故D不正确.
故选A.
点评:怕断函数的奇偶性,先看定义域是否关于原点对称,若对称,由f(-x)=-f(x)知函数为定义域上的奇函数,由f(-X)=f(x)知函数为定义域上的偶函数;若定义域不关于原点对称,在定义域内函数是非奇非偶的.有时也可以根据函数图象的特点分析,函数图象关于原点中心对称是函数为奇函数的充要条件,关于y轴轴对称是函数为偶函数的充要条件.
分析:四个选项中都给出了具体的函数解析式,其中选项A是分段函数,可由f(-x)=-x|-x|=-x|x|=-f(x)知函数为奇函数,在分析x>0时函数的增减性,根据奇函数的对称性进一步得到函数在整个定义域内的增减性;
选项B举一反例即可;
C、D中的两个函数,定义域均不关于原点对称,都不是奇函数.
解答:由f(-x)=-x|-x|=-x|x|=-f(x),知函数f(x)=x|x|为奇函数,又f(x)=x|x|=
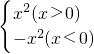 当x>0时,f(x)=x2在(0,∞)上为增函数,根据奇函数图象关于原点中心对称,
当x>0时,f(x)=x2在(0,∞)上为增函数,根据奇函数图象关于原点中心对称,所以当x<0时,f(x)=-x2在(-∞,0)上也为增函数,所以函数f(x)=x|x|在定义域内既是奇函数,又是增函数,故A正确.
∵2>1,而-23<-13,所以函数f(x)=x3在定义域内不是增函数,故B不正确.
∵
 不关于原点对称,∴f(x)=sinx
不关于原点对称,∴f(x)=sinx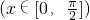 在给定的定义域内不是奇函数,故C不正确.
在给定的定义域内不是奇函数,故C不正确.∵f(x)=
 的定义域为{x|x>0},不关于原点对称,所以函数f(x)=
的定义域为{x|x>0},不关于原点对称,所以函数f(x)= 在定义域内不是奇函数,故D不正确.
在定义域内不是奇函数,故D不正确.故选A.
点评:怕断函数的奇偶性,先看定义域是否关于原点对称,若对称,由f(-x)=-f(x)知函数为定义域上的奇函数,由f(-X)=f(x)知函数为定义域上的偶函数;若定义域不关于原点对称,在定义域内函数是非奇非偶的.有时也可以根据函数图象的特点分析,函数图象关于原点中心对称是函数为奇函数的充要条件,关于y轴轴对称是函数为偶函数的充要条件.

练习册系列答案
相关题目
下列函数中,既是奇函数又是区间(0,+∞)上的增函数的是( )
A、y=x
| ||
| B、y=x-1 | ||
| C、y=x3 | ||
| D、y=2x |