题目内容
一个袋子里装有7个球,其中有红球4个,编号分别为1,2,3,4;白球3个,编号分别为2,3,4.从袋子中任取4个球(假设取到任何一个球的可能性相同).(Ⅰ)求取出的4个球中,含有编号为3的球的概率;
(Ⅱ)在取出的4个球中,红球编号的最大值设为X,求随机变量X的分布列和数学期望.
【答案】分析:(I)从7个球中取出4个球的所有可能结果数有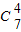 ,然后求出取出的4个球中,含有编号为3的球的结果数,代入古典概率的求解公式即可求解
,然后求出取出的4个球中,含有编号为3的球的结果数,代入古典概率的求解公式即可求解
(II)先判断随机变量X的所有可能取值为1,2,3,4,根据题意求出随机变量的各个取值的概率,即可求解分布列及期望值
解答:解:(Ⅰ) 设“取出的4个球中,含有编号为3的球”为事件A,则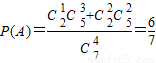
所以,取出的4个球中,含有编号为3的球的概率为 .…(5分)
.…(5分)
(Ⅱ)随机变量X的所有可能取值为1,2,3,4.…(6分)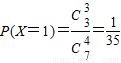 ,
,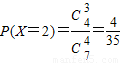 ,
,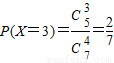 ,
,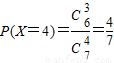 ,…(10分)
,…(10分)
所以随机变量X的分布列是
随机变量X的数学期望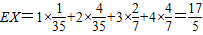 .…(14分)
.…(14分)
点评:本题主要考查了古典概型及计算公式,互斥事件、离散型随机变量的分布列及期望值的求解,考查了运用概率知识解决实际问题的能力.
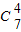 ,然后求出取出的4个球中,含有编号为3的球的结果数,代入古典概率的求解公式即可求解
,然后求出取出的4个球中,含有编号为3的球的结果数,代入古典概率的求解公式即可求解(II)先判断随机变量X的所有可能取值为1,2,3,4,根据题意求出随机变量的各个取值的概率,即可求解分布列及期望值
解答:解:(Ⅰ) 设“取出的4个球中,含有编号为3的球”为事件A,则
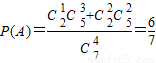
所以,取出的4个球中,含有编号为3的球的概率为
 .…(5分)
.…(5分)(Ⅱ)随机变量X的所有可能取值为1,2,3,4.…(6分)
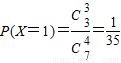 ,
,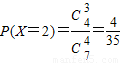 ,
,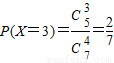 ,
,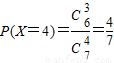 ,…(10分)
,…(10分)所以随机变量X的分布列是
| X | 1 | 2 | 3 | 4 |
| P | 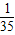 | 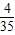 |  |  |
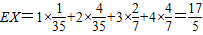 .…(14分)
.…(14分)点评:本题主要考查了古典概型及计算公式,互斥事件、离散型随机变量的分布列及期望值的求解,考查了运用概率知识解决实际问题的能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目