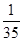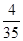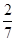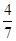题目内容
一个袋子里装有7个球,其中有红球4个, 编号分别为1，2，3，4；白球3个,编号分别为1，2，3.从袋子中任取4个球(假设取到任何一个球的可能性相同).
(Ⅰ)求取出的4个球中, 含有编号为3的球的概率；
(Ⅱ)在取出的4个球中, 红球编号的最大值设为X，求随机变量X的分布列和数学期望.
【答案】
(Ⅰ)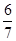
；(Ⅱ)
|
X |
1 |
2 |
3 |
4 |
|
P |
|
|
|
|
.
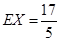【解析】
试题分析：(Ⅰ)分别算出取出四个球的取法数以及取出的4个球中含有编号为3的球的取法种数，后者与前者之比即为所求.(Ⅱ)可知随机变量X的所有可能取值为1，2，3，4.然后将每种可能取值的概率计算出，即可列出分布表.再由期望的计算公式即可得出期望.
试题解析：(Ⅰ)设“取出的4个球中，含有编号为3的球”为事件A，
由题意，取出四个球共有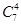
取法.其中含有编号为3的球的取法有
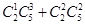种.
则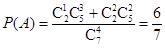
.
所以，取出的4个球中，含有编号为3的球的概率为.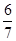
4分
(Ⅱ)随机变量X的所有可能取值为1，2，3，4.
， 
，
， 
，
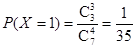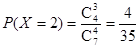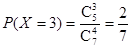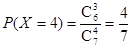8分
所以随机变量X的分布列是
|
X |
1 |
2 |
3 |
4 |
|
P |
|
|
|
|
随机变量X的数学期望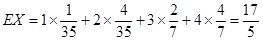
. 12分
考点：1.随机事件的概率；2.离散型随机变量及分布列；3.期望.
练习册系列答案
相关题目