题目内容

已知函数f(x)=
x2-x-2
+
1
2-|x|
，g(x)=
2x+1，-1≤x≤0
1-x2，0＜x≤1
．
（Ⅰ）求函数y=f（x）的定义域；
（Ⅱ）求g[f（3）]的值，作出函数y=g（x）的图象并指出函数y=g（x）的值域．
分析：（Ⅰ）根据函数f（x）成立的条件即可求函数y=f（x）的定义域；
（Ⅱ）根据函数表达式直接代入进行求值即可．
解答：解：（Ⅰ）依题意有
x2-x-2≥0
x≠±2
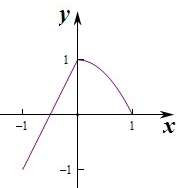
，精英家教网
即
x≥2或x≤-1
x≠±2
，
∴x∈（-∞，-2）∪（-2，-1]∪（2，+∞），
即y=f（x）的定义域为（-∞，-2）∪（-2，-1]∪（2，+∞）．     
（Ⅱ）∵f（1）=1，
∴g[f（3）]=g（1）=0．
图象：
由图象可知当-1≤x≤0时，-1≤g（x）≤1，
当0＜x≤1，0≤x＜1，
∴函数y=g（x）的值域为[-1，1]．
点评：本题主要考查函数定义域的求法以及分段函数的图象和性质，比较基础．
练习册系列答案
相关题目
已知函数f(x)=x-2m2+m+3(m∈Z)为偶函数，且f（3）＜f（5）．
（1）求m的值，并确定f（x）的解析式；
（2）若g（x）=loga[f（x）-ax]（a＞0且a≠1），是否存在实数a，使g（x）在区间[2，3]上的最大值为2，若存在，请求出a的值，若不存在，请说明理由．
（2011•上海模拟）已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．

已知函数f(x)的图像在[a，b]上连续不断，f1(x)＝min{f(t)|a≤t≤x}(x∈[a，b])，f2(x)＝max{f(t)|a≤t≤x}(x∈[a，b])，其中，min{f(x)|x∈D}表示函数f(x)在D上的最小值，max{f(x)|x∈D}表示函数f(x)在D上的最大值，若存在最小正整数k，使得f2(x)－f1(x)≤k(x－a)对任意的x∈[a，b]成立，则称函数f(x)为[a，b]上的“k阶收缩函数”．已知函数f(x)＝x2，x∈[－1，4]为[－1，4]上的“k阶收缩函数”，则k的值是_________．
已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f（x）、g（x），下列说法正确的是（ ）
A．f（x）是奇函数，g（x）是奇函数，则f（x）+g（x）是奇函数
B．f（x）是偶函数，g（x）是偶函数，则f（x）+g（x）是偶函数
C．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）一定是奇函数或偶函数
D．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）可以是奇函数或偶函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网