题目内容
5. 如图,AB为圆O的直径,E是圆O上不同于A,B的动点,四边形ABCD 为矩形,且AB=2,AD=1,平面ABCD⊥平面ABE.
如图,AB为圆O的直径,E是圆O上不同于A,B的动点,四边形ABCD 为矩形,且AB=2,AD=1,平面ABCD⊥平面ABE.(1)求证:BE⊥平面DAE;
(2)当点E在$\widehat{AB}$的什么位置时,四棱锥E-ABCD的体积为$\frac{\sqrt{3}}{3}$.
分析 (1)利用矩形的性质可得:DA⊥AB,利用面面垂直的性质定理可得:DA⊥平面ABE,利用圆的性质可得AE⊥BE,即可证明.
(2)利用面面垂直的性质与线面垂直的判定定理可得:EH⊥平面ABCD.在Rt△BAE中,设∠BAE=α(0<α<$\frac{π}{2}$),利用VE-ABCD=$\frac{1}{3}{S}_{ABCD}×HE$=$\frac{1}{3}×2×1×sin2α$=$\frac{2}{3}sin2α$=$\frac{\sqrt{3}}{3}$,解得α,即可得出点E的位置.
解答 解:(1)∵四边形ABCD为矩形,
∴DA⊥AB,
又平面ABCD⊥平面ABE,
且平面ABCD∩平面ABE=AB,
∴DA⊥平面ABE,
而BE?平面ABE,∴DA⊥BE.
又∵AB为圆O的直径,E是圆O上不同于A,B的
动点,∴AE⊥BE.
∵DA∩AE=A,∴BE⊥平面DAE.
(2)∵平面ABCD⊥平面ABE,过点E作EH⊥AB交AB于点H,则EH⊥平面ABCD.
在Rt△BAE中,设∠BAE=α(0<α<$\frac{π}{2}$),
∵AB=2,∴AE=2cosα,HE=AEsinα=2sinαcosα=sin2α,
∴VE-ABCD=$\frac{1}{3}{S}_{ABCD}×HE$=$\frac{1}{3}×2×1×sin2α$=$\frac{2}{3}sin2α$.
由已知VE-ABCD=$\frac{\sqrt{3}}{3}$,∴$\frac{2}{3}sin2α=\frac{\sqrt{3}}{3}$,化为sin2α=$\frac{\sqrt{3}}{2}$.
∵0<α<$\frac{π}{2}$,∴$2α=\frac{π}{3}$,即$α=\frac{π}{6}$;
或2$α=\frac{2π}{3}$,即$α=\frac{π}{3}$.
于是点E在$\widehat{AB}$满足$∠EAB=\frac{π}{6}$或$∠EAB=\frac{π}{3}$时,四棱锥E-ABCD的体积为$\frac{\sqrt{3}}{3}$.
点评 本题考查了线面面面垂直的判定与性质定理、圆的性质、四棱锥的体积计算公式、三角函数的计算与性质,考查了推理能力与计算能力,考查了空间想象能力,属于中档题.

| A. | 2 | B. | $\sqrt{2}$ | C. | 10 | D. | $\sqrt{10}$ |
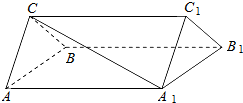 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,E为BC中点
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,E为BC中点 质地均匀的一个转盘,从圆心开始作四个半径,将圆盘分成A,B,C,D四份,它们所对的圆心角依次为45°,60°,120°,135°,端点在圆心的指针可以绕圆心转动,某人进行游戏,规则是随机转动指针,待其自行停下,指针停在A,B,C,D区域可分别得到4,3,2,1分,设指针转动后停在任何一个地方是等可能的,指针停在分界线上时,按高分计算.
质地均匀的一个转盘,从圆心开始作四个半径,将圆盘分成A,B,C,D四份,它们所对的圆心角依次为45°,60°,120°,135°,端点在圆心的指针可以绕圆心转动,某人进行游戏,规则是随机转动指针,待其自行停下,指针停在A,B,C,D区域可分别得到4,3,2,1分,设指针转动后停在任何一个地方是等可能的,指针停在分界线上时,按高分计算. 如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.
如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点. 如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC=$\frac{2}{3}$AB,又PO⊥平面ABC,DA∥PO,DA=AO=$\frac{1}{2}$PO.
如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC=$\frac{2}{3}$AB,又PO⊥平面ABC,DA∥PO,DA=AO=$\frac{1}{2}$PO.