题目内容
设实数x,y满足约束条件
|
| 1 |
| a2 |
| 1 |
| b2 |
分析:作出不等式组的可行域,将目标函数变形,作出直线由图判断出当直线平移至点A时z最大,列出方程求出ab的值,利用基本不等式求出
+
最小值.
| 1 |
| a2 |
| 1 |
| b2 |
解答: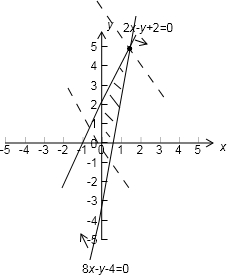 解:画出不等式组
解:画出不等式组
的可行域
将z=abx+y变形为y=-abx+z,
由图知,当直线过A点时纵截距最大,z最大
由
得(1,4)代入目标函数,最大值为ab+4
所以ab+4=8
所以ab=4
∴
+
≥2
=1
当且仅当a=b时取等号
故答案为1
 解:画出不等式组
解:画出不等式组
|
将z=abx+y变形为y=-abx+z,
由图知,当直线过A点时纵截距最大,z最大
由
|
所以ab+4=8
所以ab=4
∴
| 1 |
| a2 |
| 1 |
| b2 |
|
当且仅当a=b时取等号
故答案为1
点评:利用线性规划求函数的最值关键是给目标函数几何意义;利用基本不等式求函数的最值一定要注意满足的条件:一正、二定、三相等.

练习册系列答案
相关题目