题目内容
设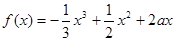 .
.
(1)若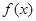 在
在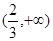 上存在单调递增区间,求
上存在单调递增区间,求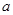 的取值范围;
的取值范围;
(2)当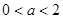 时,
时,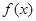 在
在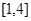 上的最小值为
上的最小值为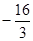 ,求
,求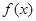 在该区间上
在该区间上
的最大值.
【答案】
解:(1)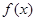 在
在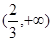 上存在单调递增区间,即存在某个子区间
上存在单调递增区间,即存在某个子区间 使得
使得 .由
.由 ,
,
由于导函数 在区间
在区间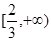 上单调递减,则只需
上单调递减,则只需 即可。
即可。
由 解得
解得 ,
,
所以 当 时,
时,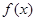 在
在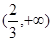 上存在单调递增区间. ……………6分
上存在单调递增区间. ……………6分
(2)令 ,得两根
,得两根 ,
,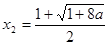 .
.
所以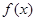 在
在 ,
, 上单调递减,在
上单调递减,在 上单调递增…………8分
上单调递增…………8分
当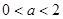 时,有
时,有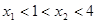 ,所以
,所以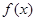 在
在 上的最大值为
上的最大值为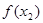
又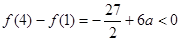 ,即
,即 ……………10分
……………10分
所以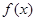 在
在 上的最小值为
上的最小值为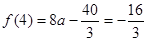 ,得
,得 ,
,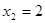 ,
,
从而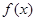 在
在 上的最大值为
上的最大值为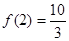 .
.
【解析】略

练习册系列答案
相关题目

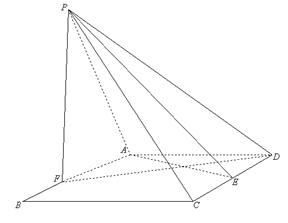
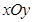 中,已知点
中,已知点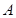
 ,点P是动点,且三角形
,点P是动点,且三角形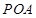 的三边所在直线
的三边所在直线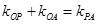 .
.
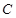 的方程;
的方程;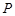 的一个点,若
的一个点,若 ,直线
,直线 与
与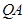 交于点M,探究是否存点P使得
交于点M,探究是否存点P使得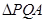 和
和 的面积满足
的面积满足 ,若存在,求出点P的坐标;若不存在,说明理由.
,若存在,求出点P的坐标;若不存在,说明理由. 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点
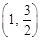 .
. (2,1)的直线
(2,1)的直线 与椭圆
与椭圆 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 ,由题意得
,由题意得

 ,代入椭圆
,代入椭圆 .
. ,
,
 .解得。
.解得。 .……………………4分
.……………………4分 .
.
 ,
, ,
,
 .
. .
. ,解得
,解得 .
.