题目内容
如图，圆O是以AB为直径的△ABC的外接圆，点D是劣弧
的中点，连接AD并延长，与过C点的切线交于点P,OD与BC相交于点E
（1）求证：
（2）求证：
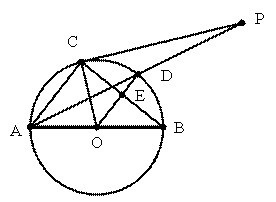
证明：（1）因为AB为圆O的直径，所以AC⊥BC，又D是劣弧的中点，
由垂径定理得OD⊥BC,因此OD∥AC,
又因为点O为AB的中点，所以 …………………6分
（2）连接CD,因为PC是圆O的切线，所以∠PCD=∠PAC,又因为∠P是公共角，所以△PCD∽△PAC 得
又D是劣弧的中点，所以CD=BD 所以
…………12分
练习册系列答案
相关题目
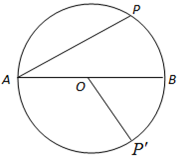如图，点P是以AB为直径的圆O上动点，P'是点P关于AB的对称点，AB=2a（a＞0）．
（2012•潍坊二模）如图，点C是以AB为直径的圆上一点，直角梯形BCDE所在平面与圆O所在平面垂直，且DE∥BC，DC⊥BC，DE=
的中点，连接AD并延长，与过C点的切线交于点P，OD与BC相交于点E
BC=2，AC=CD=3．