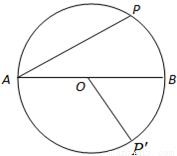
题目内容
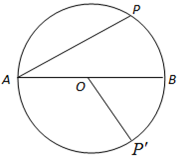 如图,点P是以AB为直径的圆O上动点,P'是点P关于AB的对称点,AB=2a(a>0).
如图,点P是以AB为直径的圆O上动点,P'是点P关于AB的对称点,AB=2a(a>0).(Ⅰ)当点P是弧
 |
| AB |
| AP |
| AB |
(Ⅱ)求
| AP |
| OP′ |
分析:(Ⅰ)由已知先求出点P的坐标,再利用数量积即可求出;
(Ⅱ)设∠POB=θ,θ∈[0,2π),写出点p与P′的坐标,求出
•
的表达式,再利用二次函数和余弦函数的单调性即可求出其最值.
(Ⅱ)设∠POB=θ,θ∈[0,2π),写出点p与P′的坐标,求出
| AP |
| AP′ |
解答:解:(Ⅰ)以直径AB所在直线为x轴,以O为坐标原点建立平面直角坐标系.
∵P是弧AB靠近点B的三等分点,
连接OP,则∠BOP=
,
点P坐标为(
a,
a).
又点A坐标是(-a,0),点B坐标是(a,0),
∴
=(
a,
a),
=(2a,0),
∴
•
=3a2.
(Ⅱ)设∠POB=θ,θ∈[0,2π),则P(acosθ,asinθ),
P'(acosθ,-asinθ),
∴
=(acosθ+a,asinθ),
=(acosθ,-asinθ).
∴
•
=a2cos2θ+a2cosθ-a2sin2θ=a2(2cos2θ+cosθ-1)
=2a2(cos2θ+
cosθ+
)-
a2=2a2(cosθ+
)2-
a2.
当cosθ=-
时,
•
有最小值-
a2,
当cosθ=1时,
•
有最大值2a2.
∵P是弧AB靠近点B的三等分点,
连接OP,则∠BOP=
| π |
| 3 |

点P坐标为(
| 1 |
| 2 |
| ||
| 2 |
又点A坐标是(-a,0),点B坐标是(a,0),
∴
| AP |
| 3 |
| 2 |
| ||
| 2 |
| AB |
∴
| AP |
| AB |
(Ⅱ)设∠POB=θ,θ∈[0,2π),则P(acosθ,asinθ),
P'(acosθ,-asinθ),
∴
| AP |
| OP′ |
∴
| AP |
| OP′ |
=2a2(cos2θ+
| 1 |
| 2 |
| 1 |
| 16 |
| 9 |
| 8 |
| 1 |
| 4 |
| 9 |
| 8 |
当cosθ=-
| 1 |
| 4 |
| AP |
| OP′ |
| 9 |
| 8 |
当cosθ=1时,
| AP |
| OP′ |
点评:熟练掌握圆的对称性、向量的数量积、三角函数和二次函数的单调性是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目

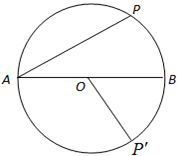 如图,点P是以AB为直径的圆O上动点,P'是点P关于AB的对称点,AB=2a(a>0).
如图,点P是以AB为直径的圆O上动点,P'是点P关于AB的对称点,AB=2a(a>0). 上靠近B的三等分点时,求
上靠近B的三等分点时,求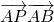 的值;
的值;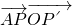 的最大值和最小值.
的最大值和最小值.
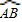 上靠近B的三等分点时,求
上靠近B的三等分点时,求 的值;
的值; 的最大值和最小值.
的最大值和最小值.