题目内容
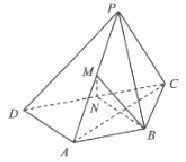
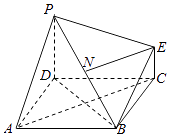
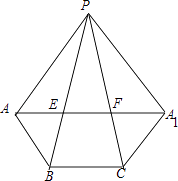
【题目】如图,已知正三棱锥P﹣ABC的底面边长为4,侧棱长为8,E,F分别为PB,PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P﹣AEF的体积. 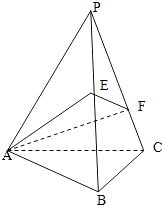
【答案】解:如图,沿棱AB,AC,PA剪开,得到正三棱锥的侧面展开图,
则AA1的长为△BEF的周长的最小值.
由平面几何知识可证△PAE≌△PA1F,于是PE=PF,
又PB=PC,故EF∥BC.
∵∠ABE=∠PBC,∠AEB=∠PCB,
∴△ABE∽△PBC,
∴ ![]() ,
,
∴BE=2,
AE=A1F=4,PE=8﹣2=6.
由EF∥BC,有 ![]() ,
,
∴ ![]() ,
,
∴AA1=AE+EF+A1F=4+3+4=11,
∴△AEF周长的最小值是11,此时 ![]() ,即E,F分别在PB,PC的四等分点处.
,即E,F分别在PB,PC的四等分点处.
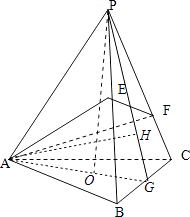
取BC中点G,连AG、PG,过P作PO⊥AG,垂足为O,则PO⊥平面ABC,
过A作AH⊥PG,垂足为H,则AH⊥平面PBC.
在Rt△PAO中,OA= ![]() ,
,
在Rt△PBG中,PG= ![]() ,又
,又 ![]() ,
,
由等积原理可得, ![]() ,
,
由于E、F是PB、PC的四等分点,
∴S△PEF= ![]() ,
,
∴ ![]() =
= ![]() .
.
【解析】沿棱AB、AC、PA剪开,得到正三棱锥的侧面展开图,在平面图形中,利用平面几何知识可得EF∥BC,再由△ABE∽△PBC,结合相似三角形对应边成比例及平行线截线段成比例定理求得截面△AEF周长的最小值;由△AEF周长取最小值时E,F分别在PB,PC的四等分点处.可得三角形PEF面积与三角形PBC面积的关系,再求出A到侧面PBC的距离,利用等积法可得三棱锥P﹣AEF的体积.

练习册系列答案
相关题目