题目内容
已知三角形三边所在直线的方程为x-y+2=0,x-3y+4=0,x+y-4=0,求三角形外接圆的方程.
解:设三角形的三个顶点分别为A、B、C,圆的方程为x2+y2+Dx+Ey+F=0;
由题意知,由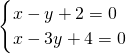 ,顶点A的坐标(-1,1);
,顶点A的坐标(-1,1);
同理可求B(1,3)、C(2,2).
把顶点A、B、C坐标代入圆的方程得,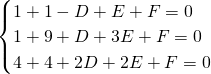 ,
,
解得D=-1,E=-3,F=0,
故三角形外接圆的方程为:x2+y2-x-3y=0.
分析:由题意分别联立三条直线方程,可求得三角形顶点坐标,设圆的方程为一般式,把三点坐标代入列方程组,求出系数.
点评:本题考查了联立直线方程求交点坐标,用待定系数法求圆的方程,通常用一般式方程计算要简单.
由题意知,由
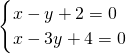 ,顶点A的坐标(-1,1);
,顶点A的坐标(-1,1);同理可求B(1,3)、C(2,2).
把顶点A、B、C坐标代入圆的方程得,
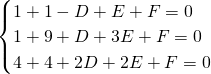 ,
,解得D=-1,E=-3,F=0,
故三角形外接圆的方程为:x2+y2-x-3y=0.
分析:由题意分别联立三条直线方程,可求得三角形顶点坐标,设圆的方程为一般式,把三点坐标代入列方程组,求出系数.
点评:本题考查了联立直线方程求交点坐标,用待定系数法求圆的方程,通常用一般式方程计算要简单.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
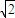 =0,则这个三角形内切圆的方程为 .
=0,则这个三角形内切圆的方程为 .