题目内容
已知三角形三边所在直线的方程为y=0,x=2,x+y-4-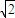 =0,则这个三角形内切圆的方程为 .
=0,则这个三角形内切圆的方程为 .
【答案】分析:设出圆心坐标、半径,圆心到三条直线距离相等,解出圆心、半径即可得到结果.
解答: 解:由题意可知所求圆的圆心在第一象限,设所求圆的圆心坐标(2+b,b),半径为b,
解:由题意可知所求圆的圆心在第一象限,设所求圆的圆心坐标(2+b,b),半径为b,
则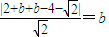 ,|2b-2-
,|2b-2-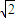 |=
|=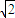 b,即:2b-2-
b,即:2b-2-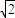 =±
=±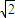 b
b
解得b=1,或b=3+2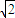 ,(当b=3+2
,(当b=3+2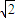 时,因为圆心不在三角形内,舍去)如图
时,因为圆心不在三角形内,舍去)如图
则这个三角形内切圆的方程为:(x-3)2+(y-1)2=1
故答案为:(x-3)2+(y-1)2=1.
点评:本题考查圆的标准方程,是基础题.
解答:
 解:由题意可知所求圆的圆心在第一象限,设所求圆的圆心坐标(2+b,b),半径为b,
解:由题意可知所求圆的圆心在第一象限,设所求圆的圆心坐标(2+b,b),半径为b,则
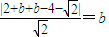 ,|2b-2-
,|2b-2-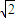 |=
|=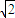 b,即:2b-2-
b,即:2b-2-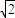 =±
=±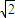 b
b解得b=1,或b=3+2
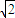 ,(当b=3+2
,(当b=3+2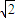 时,因为圆心不在三角形内,舍去)如图
时,因为圆心不在三角形内,舍去)如图则这个三角形内切圆的方程为:(x-3)2+(y-1)2=1
故答案为:(x-3)2+(y-1)2=1.
点评:本题考查圆的标准方程,是基础题.

练习册系列答案
相关题目