题目内容
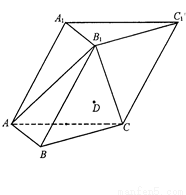
如图,在各棱长均为 的三棱柱
的三棱柱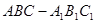 中,侧面
中,侧面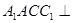 底面
底面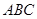 ,
,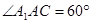 .
.
(1)求侧棱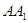 与平面
与平面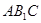 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)已知点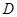 满足
满足 ,在直线
,在直线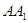 上是否存在点
上是否存在点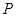 ,使
,使 ?若存在,请确定点
?若存在,请确定点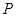 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】
(1)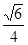 (2)存在点
(2)存在点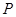 ,使
,使 ,其坐标为
,其坐标为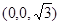 ,即恰好为
,即恰好为 点.
点.
【解析】
试题分析:(1)∵侧面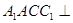 底面
底面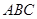 ,作
,作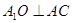 于点
于点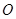 ,∴
,∴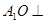 平面
平面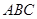 .
.
又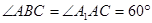 ,且各棱长都相等,∴
,且各棱长都相等,∴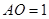 ,
,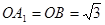 ,
,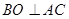 .
2分
.
2分
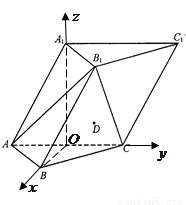
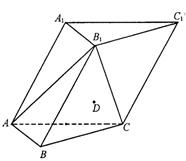
故以 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系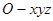 ,则
,则
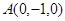 ,
,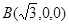 ,
,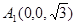 ,
,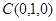 ,
,
∴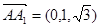 ,
, ,
,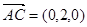 .……4分
.……4分
设平面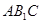 的法向量为
的法向量为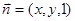 ,则
,则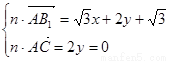
解得 .由
.由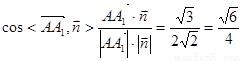 .
.
而侧棱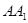 与平面
与平面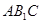 所成角,即是向量
所成角,即是向量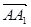 与平面
与平面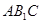 的法向量所成锐角的余角,
的法向量所成锐角的余角,
∴侧棱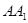 与平面
与平面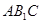 所成角的正弦值的大小为
所成角的正弦值的大小为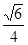 6分
6分
(2)∵ ,而
,而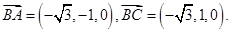
∴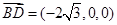
又∵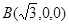 ,∴点
,∴点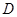 的坐标为
的坐标为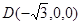 .
.
假设存在点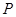 符合题意,则点
符合题意,则点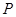 的坐标可设为
的坐标可设为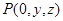 ,∴
,∴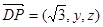 .
.
∵ ,
, 为平面
为平面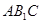 的法向量,
的法向量,
∴由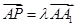 ,得
,得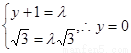 . 10分
. 10分
又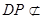 平面
平面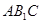 ,故存在点
,故存在点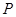 ,使
,使 ,其坐标为
,其坐标为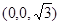 ,
,
即恰好为 点.
12分
点.
12分
考点:本题考查了空间中的线面关系
点评:运用向量在解决立体几何问题主要集中在法向量的应用上,它可以证明空间线面的位置关系、求解空间角、距离.同时运用空间向量解答立体几何问题,淡化了传统立体几何中的“形”的推理方法,强化了代数运算,从而降低了思维难度

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
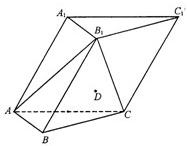 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.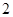 的三棱柱
的三棱柱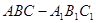 中,侧面
中,侧面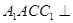 底面
底面 ,
,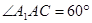 .
.
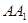 与平面
与平面 所成角的正弦值的大小;
所成角的正弦值的大小;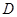 满足
满足 ,在直线
,在直线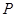 ,使
,使 ?若存在,请确定点
?若存在,请确定点 B
B ,在直线AA
,在直线AA