题目内容
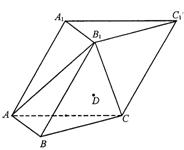
如图,在各棱长均为2的三棱柱ABC-A B
B C
C 中,侧面A
中,侧面A ACC
ACC ⊥底面ABC,∠A
⊥底面ABC,∠A AC=60°.
AC=60°.
(Ⅰ)求侧棱AA 与平面AB
与平面AB C所成角的正弦值的大小;
C所成角的正弦值的大小;
(Ⅱ)已知点D满足 ,在直线AA
,在直线AA 上是否存在点P,使DP∥平面AB
上是否存在点P,使DP∥平面AB C?若存在,请确定点P的位置;若不存在,请说明理由.
C?若存在,请确定点P的位置;若不存在,请说明理由.

【答案】
解:(Ⅰ)∵侧面A1ACC1⊥底面ABC,作A1O⊥AC于点O,
∴A1O⊥平面ABC.又∠ABC=∠A1AC=60°,且各棱长都相等,
∴AO=1,OA1=OB= ,BO⊥AC.
,BO⊥AC.
故以O为坐标原点,建立如图所示的空间直角坐标系O-xyz,则
A(0,-1,0),B( ,0,0),A1(0,0,
,0,0),A1(0,0, ),C(0,1,0),
),C(0,1,0),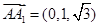 ;
;
∴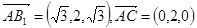 .设平面AB1C的法向量为n=(x,y,1)
.设平面AB1C的法向量为n=(x,y,1)
则 解得n=(-1,0,1).
解得n=(-1,0,1).
由cos< >=
>=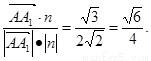
而侧棱AA1与平面AB1C所成角,即是向量 与平面AB1C的法向量所成锐角的余角,
与平面AB1C的法向量所成锐角的余角,
∴侧棱AA1与平面AB1C所成角的正弦值的大小为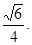
(Ⅱ)∵ 而
而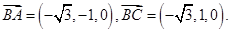 ∴
∴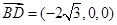
又∵B( ,0,0),∴点D的坐标为D(-
,0,0),∴点D的坐标为D(- ,0,0).假设存在点P符合题意,
,0,0).假设存在点P符合题意,
则点P的坐标可设为P(0,y,z). ∴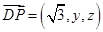
∵DP∥平面AB1C,n=(-1,0,1)为平面AB1C的法向量,
∴由 ,得
,得
又DP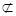 平面AB1C,故存在点P,使DP∥平面AB1C,其从标为(0,0,
平面AB1C,故存在点P,使DP∥平面AB1C,其从标为(0,0, ),即恰好为A1点
),即恰好为A1点
【解析】略

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
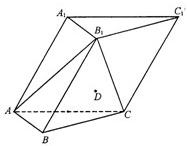 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.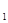 B
B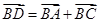 ,在直线AA
,在直线AA