题目内容

若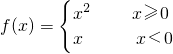 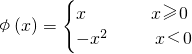$数学公式$ ， $数学公式$ 则当x＜0时，f[φ（x）]为

A.
-x
B.
-x²
C.
x
D.
x²

B
分析：由于x＜0时，φ（x）=-x²＜0，则f[φ（x）]=f（-x²）=-x²，即可得到正确结论．
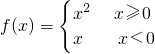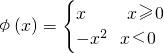解答：由于 $\text{[math]}$ ， $\text{[math]}$ ，
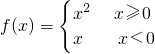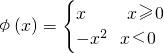则当x＜0时，φ（x）=-x²
∵x＜0，∴-x²＜0
所以f[φ（x）]=f（-x²）=-x²
故答案为 B
点评：本题考查函数值的求解问题，属于基础题．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

给出下列四个命题：
①命题“?x∈R，cosx＞0”的否定是“?x∈R，cosx≤0”；
②若0＜a＜1，则函数f（x）=x²-a^x-3只有一个零点；
③若lga+lgb=lg（a+b），则a+b的最小值为4；
④对于任意实数x，有f（-x）=f（x），且当x＞0时，f′（x）＞0，则当x＜0时，f′（x）＜0．
其中正确命题的序号是

．（填所有正确命题的序号）

（2012•安徽模拟）若函数f（x）为奇函数，且当x＞0时，f（x）=2x-3，则当x＜0时，f（x）=（　　）

A．f（x）=-2x+3

B．f（x）=-3x+2

C．f（x）=2x+3

D．f（x）=3x+2

若函数f（x）满足f（-x）=f（x），并且当x＞0时，f（x）=x+1，则当x＜0时，f（x）=

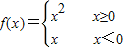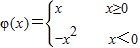则当x＜0时，f[φ（x）]为（）
A．-
B．-x²
C．
D．x²