题目内容
已知三个不等式：①x2-4x+3＜0；②x2-6x+8＞0；③2x2-8x+m≤0．要使同时满足①式和②式的所有x的值都满足③式，则实数m的取值范围是（ ）A．m＞9
B．m=9
C．m≤6
D．0＜m≤9
【答案】分析：联立不等式组求解满足①②的x的取值范围，根据满足①式和②式的所有x的值都满足③式可得不等式2x2-8x+m≤0对于x∈（1，2）上恒成立，列式后可求解m的范围．
解答：解：由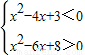
，得1＜x＜2．
若同时满足①式和②式的所有x的值都满足③式，
说明不等式2x2-8x+m≤0对于x∈（1，2）上恒成立，
即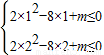
，解得m≤6．
故选C．
点评：本题考查了一元二次不等式的解法，考查了数学转化思想方法，训练了“三个二次”的结合，是中档题．
解答：解：由
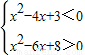，得1＜x＜2．若同时满足①式和②式的所有x的值都满足③式，
说明不等式2x2-8x+m≤0对于x∈（1，2）上恒成立，
即
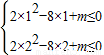，解得m≤6．故选C．
点评：本题考查了一元二次不等式的解法，考查了数学转化思想方法，训练了“三个二次”的结合，是中档题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目